A spring is loaded with two blocks and , where is rigidly fixed with the spring and just kept on the block as shown in the figure. The maximum energy of oscillation that is possible for the system having the block in contact with is

The correct Answer is:D
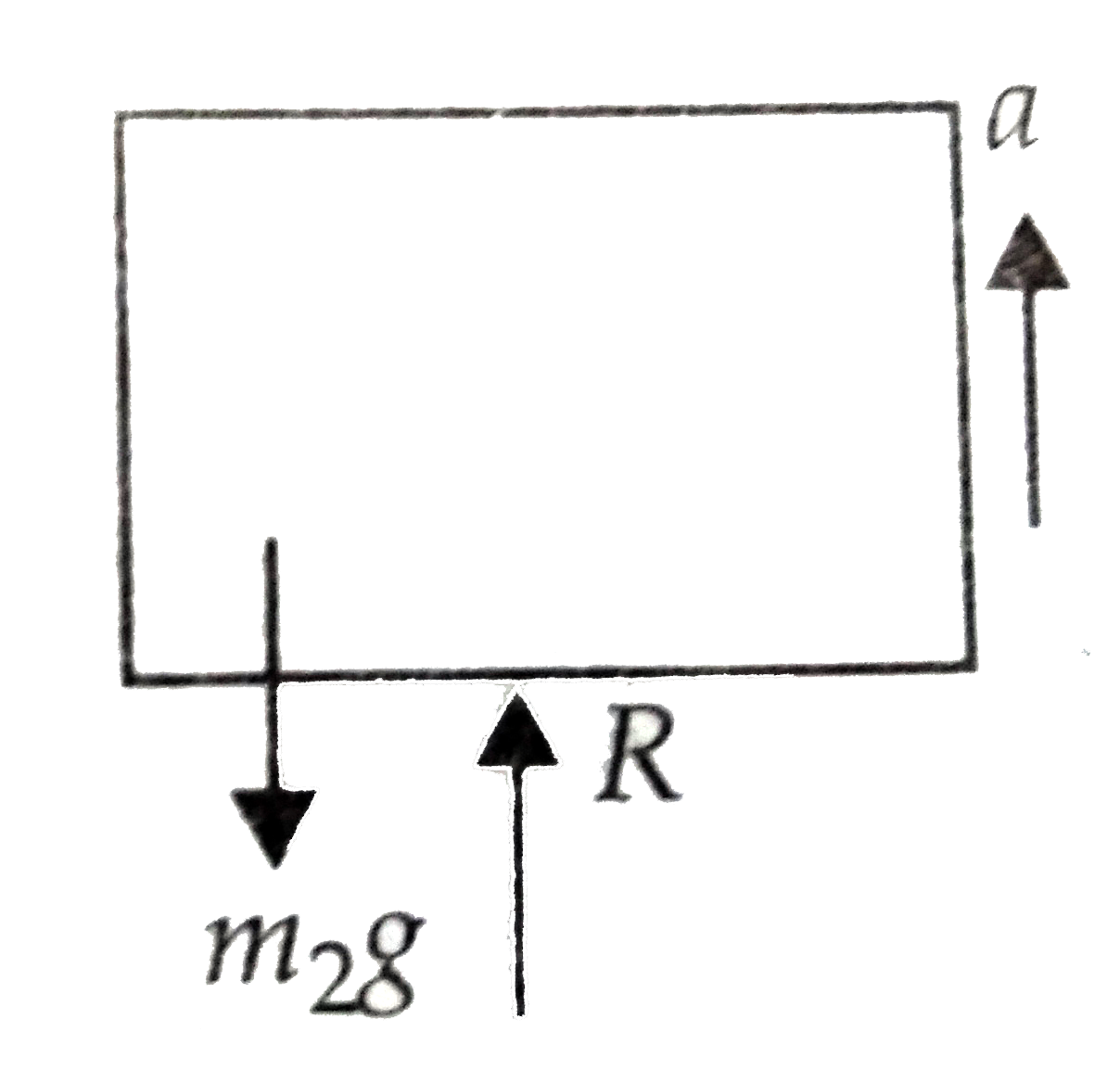
let x be the required amplitude of oscillation for this amplitude of oscillation the normal contact force between the blocks can be given by
where, acceleration
For maximum amplitude of
oscillation without loosing contact
of block with block , R=0
we get,
Where is the angular frequency of oscillation of and spring. therefore
or
Hence, the maximum energy of oscillation
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion & Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A spring is loaded with two blocks m1 and m2 where m1 is rigidly fixed with the spring and m2 is just kept on the block m1. The maximum energy of oscillation is possible for the system having the block m2 in constant with m1 is
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A spring is loaded with two blocks m1 and m2, where m1 is rigidly fixed with the spring and m2 just kept on the block m1 as shown in the figure. The maximum energy of oscillation that is possible for the system having the block m2 in contact with m1 is
 Am21g2kBm1g22kCm22g22kD(m1+m2)2g22k
Am21g2kBm1g22kCm22g22kD(m1+m2)2g22k
Two block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
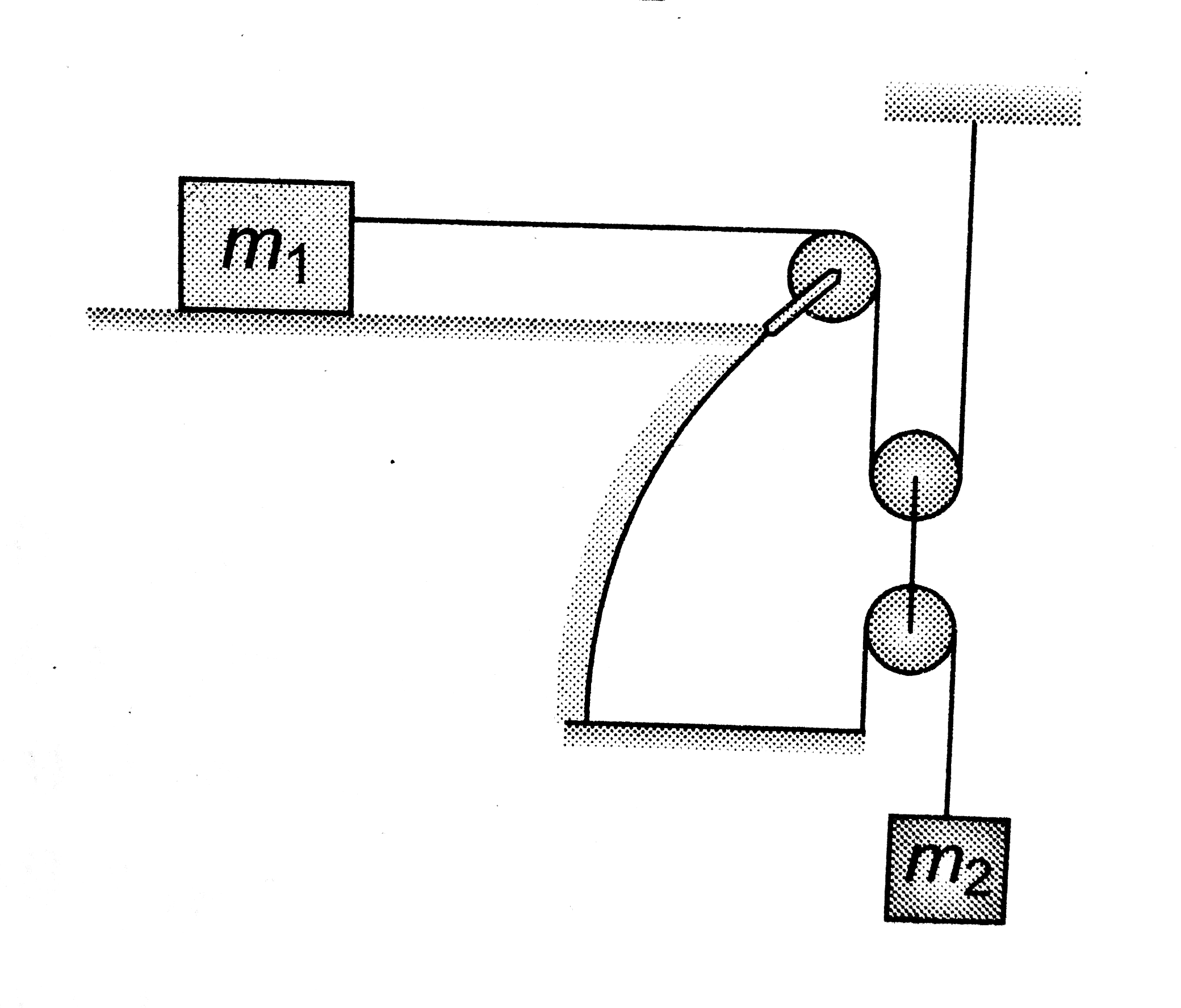
View Solution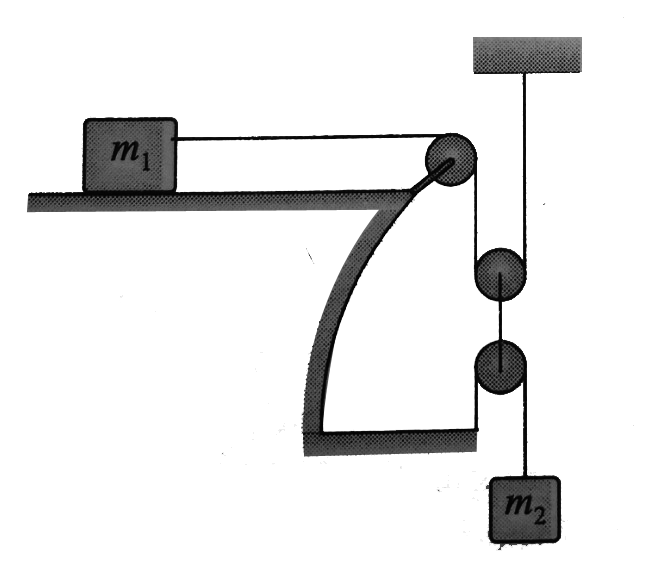
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
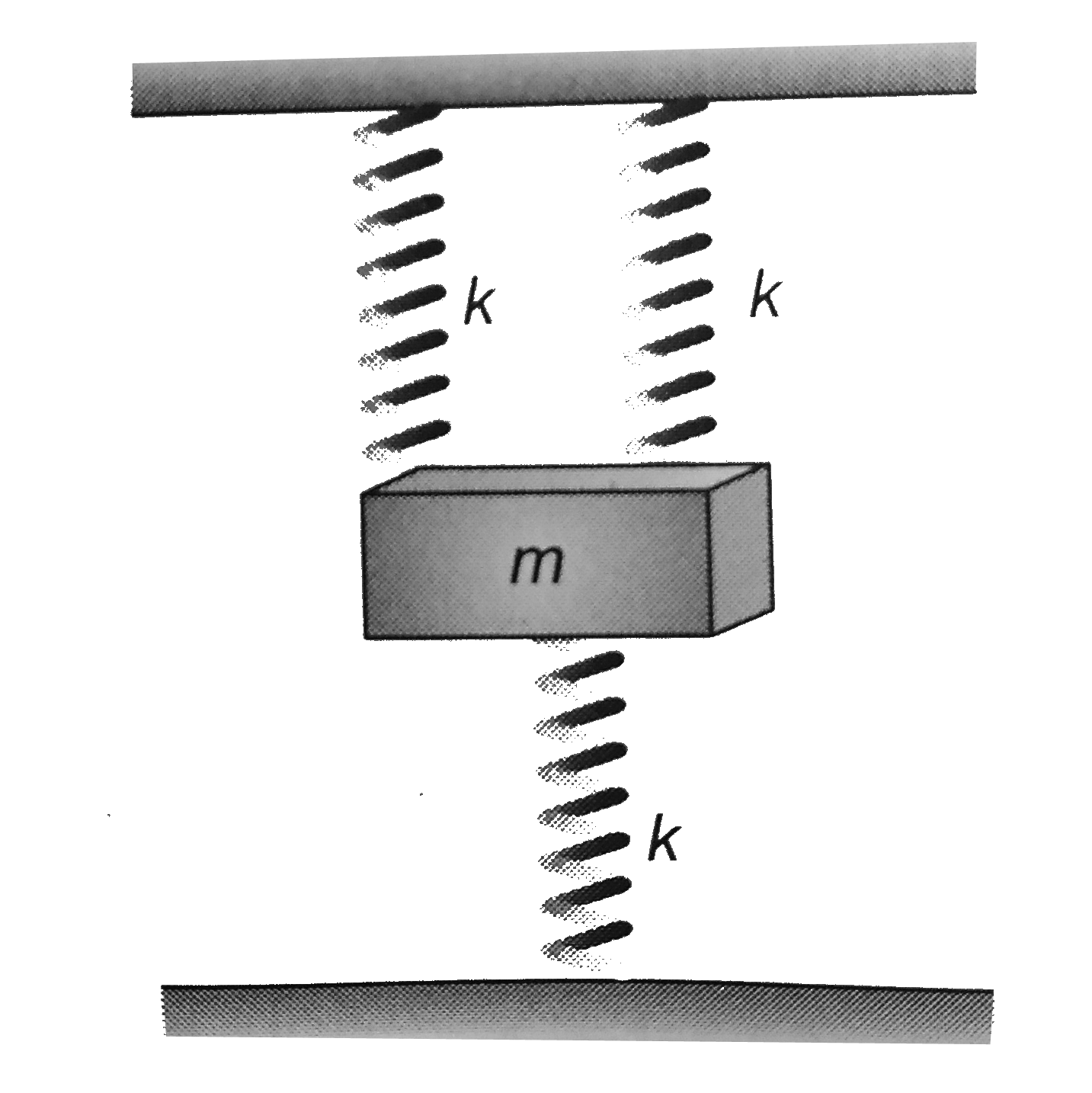
View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth plane .find the value of spring force .
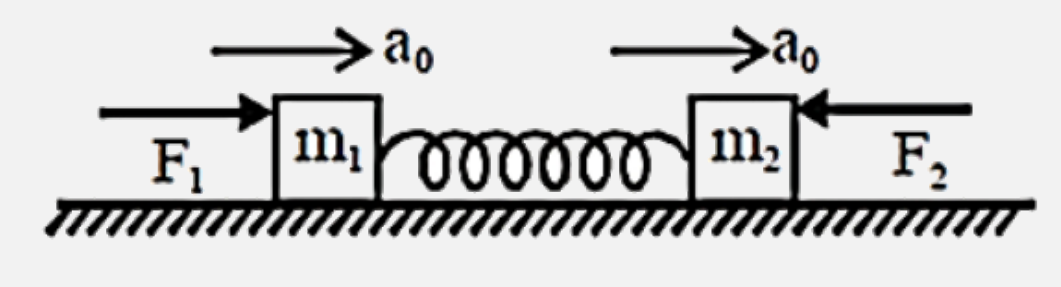
View SolutionBlocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
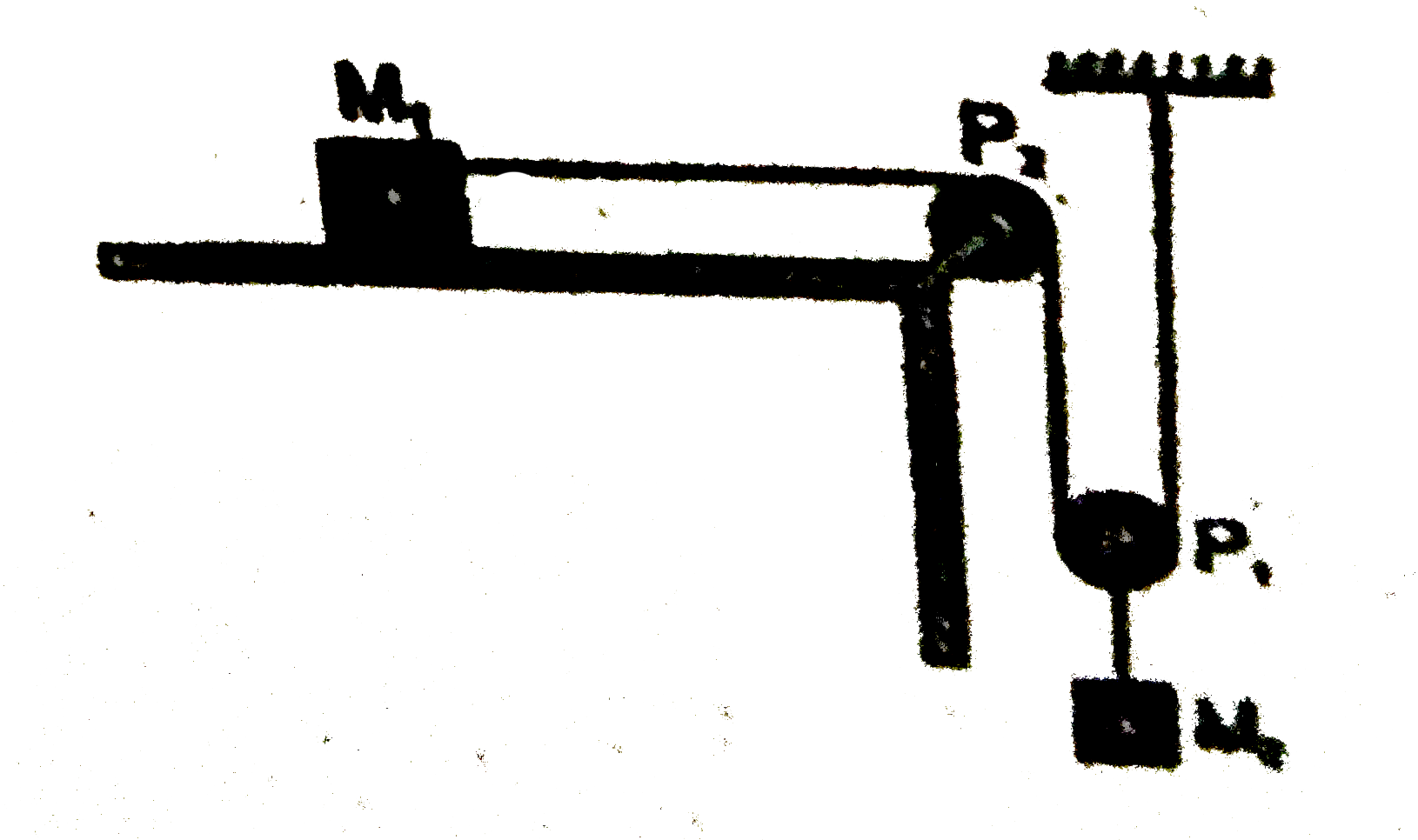
View SolutionTwo springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :
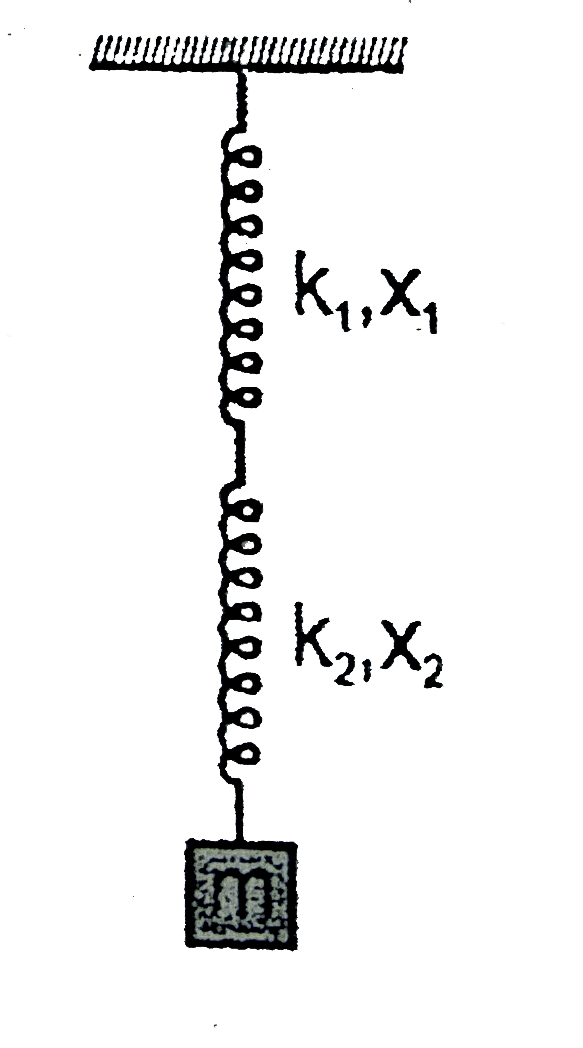
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
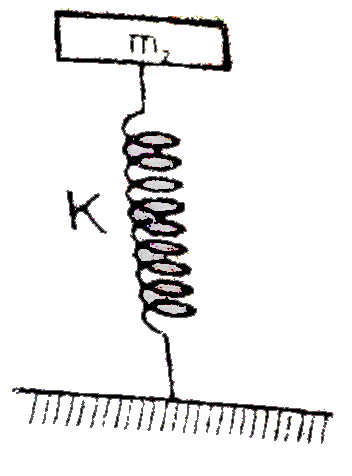
View Solution
