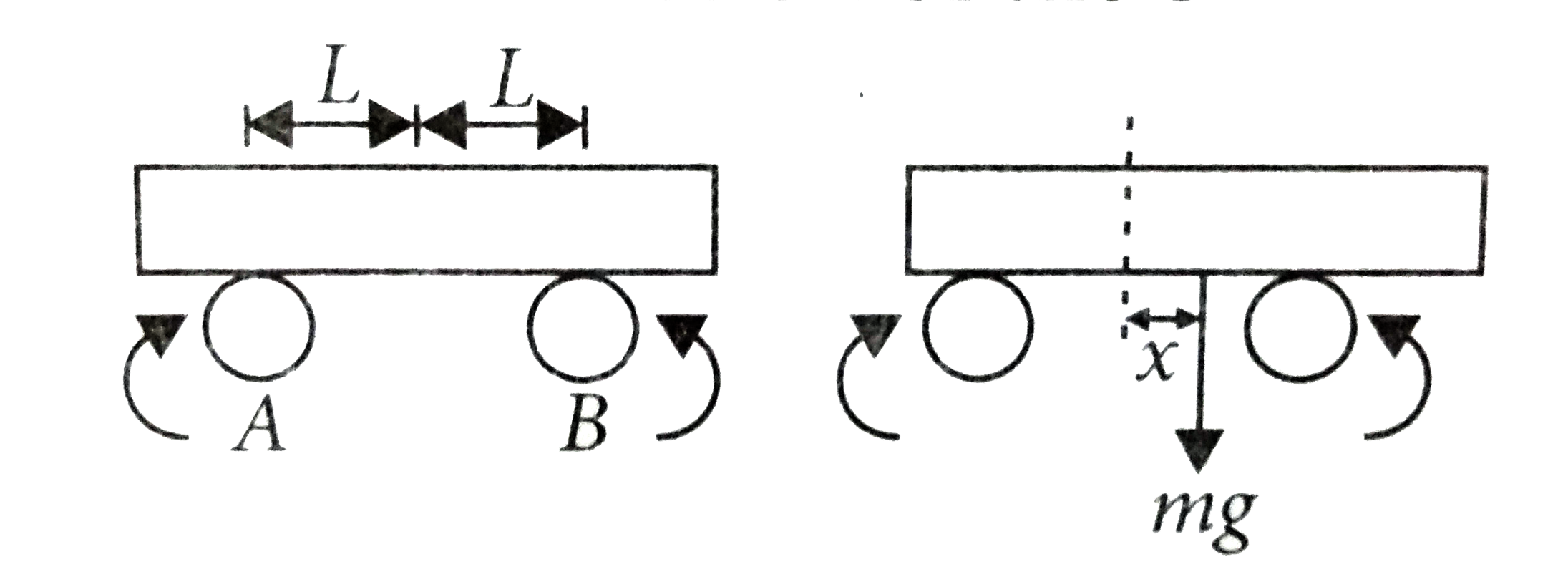
A uniform bar with mass m lies symmetrically across two rapidly rotating fixed rollers, A and B with distance L=2.0 cm between the bar's centre of mass and each roller. The rollers, whose directions of rotation are shown in figures slip against the bar with coefficient of kinetic friction μk=0.40. suppose the bar is displaced horizontally by the distance x as shown in figure and then released. the angular frequency ω of the resulting horizontal simple harmonic motion of the bar is (in rad s−1)
20
15
16
17
The correct Answer is:A
Consider horizontal forces
μkNA−μkNB=ma
or a=μkNA−μkNBm . . . (i)
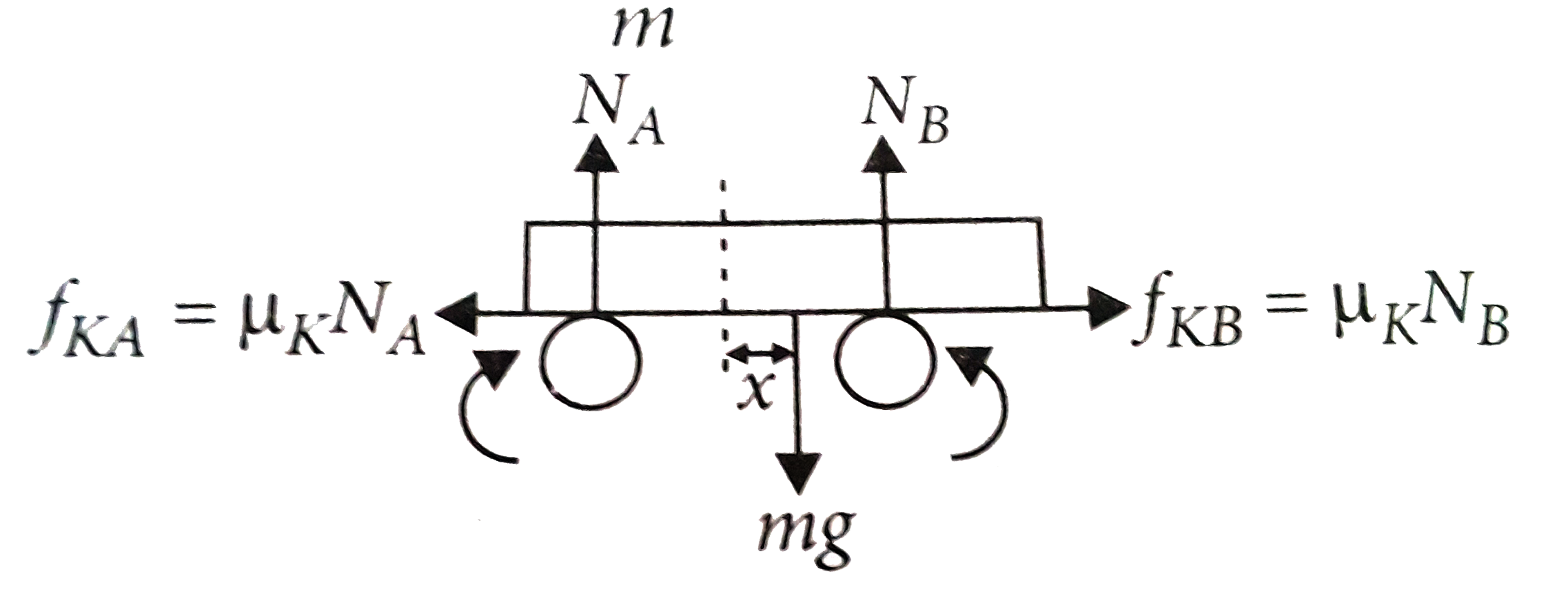
Taking torque about an axis perpendicular to the plane and through the contact point between bar and roller A. the bar experiences no angular acceleration about that axis.
NA(0)+NB(2L)−Mg(L+x)fKA(0)+kKB(0)=0 . . . (ii)
By balancing vertical forces, we have
NA+NB−mg=0 . . . (iii)
solving eqns. (i), (ii) and (iii)
NB=mg(L+X)2L,NA=mg(L−X)2L,a=−μkgLX
Comparing it with a=−ω2X
we get, ω=√μkgL=√0.40×102×10−2=14 rad s−1
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion & Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A uniform bar with mass m lies symmetrically across two rapidly rotating fixed rollers. A and B with distance 'l' between the bars centre of mass and each roller. The rollers whose direction of rotation are shown in figure slip against the bar with coefficient of friction μ. Suppose the bar is displaced horizontally by a small distance 'x' and then released, find the time period of oscillation.
View SolutionA small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is?

View Solutionthe position vector of the centre of mass lt
→
r cm of an asymmetric uniform bar of negligible area of cross - section as shown in figure is :
View SolutionTwo bar of identical dimensions are kept as shown in figure. If K1 and K2are their coefficients of thermal conductivities, then equivalent K

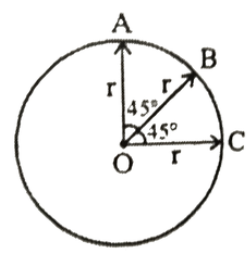
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
View SolutionTwo identical bar magnets, each of magnetic moment M, are placed as shown in figure. Magnetic field at point
View SolutionTwo bars of radius r and 2r are kept in constant as shown in figure. An electric current I is passed through the bars. Which of the following is correct?

View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View SolutionA thin bar of mass m and length l is free to rotate about a fixed horizontal axis through a point at its end.The bar is brought to a horizontal position. (θ=90∘) and then released. The angular velocity when it reaches the lowest point is
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution
