A 10 V battery connected to 5ω resistance coil having inductance 10 H through a switch drives a constant current in the circuit. The switch is suddenly opened and the time taken to open it is 2ms. The average emf induced across the coil is
4×104V
2×104V
2×102V
1×104V
The correct Answer is:D
To find the average emf induced across the coil when the switch is opened, we can follow these steps:
Step 1: Calculate the Initial Current (I1)
The initial current in the circuit can be calculated using Ohm's law:
I1=ER
Where:
- E=10V (emf of the battery)
- R=5Ω (resistance)
Substituting the values:
I1=10V5Ω=2A
Step 2: Determine the Final Current (I2)
When the switch is opened, the current drops to zero:
I2=0A
Step 3: Calculate the Change in Current (di)
The change in current (di) is:
di=I2−I1=0−2=−2A
Step 4: Calculate the Time Interval (dt)
The time taken to open the switch is given as:
dt=2ms=2×10−3s
Step 5: Calculate the Rate of Change of Current (di/dt)
The rate of change of current (didt) can be calculated as:
didt=didt=−2A2×10−3s=−1000A/s
Step 6: Calculate the Induced EMF (E)
Using the formula for induced emf in an inductor:
E=−Ldidt
Where:
- L=10H (inductance)
Substituting the values:
E=−10H×(−1000A/s)=10000V=104V
Final Answer
The average emf induced across the coil is:
Average EMF=104V
---
The initial current in the circuit can be calculated using Ohm's law:
I1=ER
Where:
- E=10V (emf of the battery)
- R=5Ω (resistance)
I1=10V5Ω=2A
When the switch is opened, the current drops to zero:
I2=0A
The change in current (di) is:
di=I2−I1=0−2=−2A
The time taken to open the switch is given as:
dt=2ms=2×10−3s
The rate of change of current (didt) can be calculated as:
didt=didt=−2A2×10−3s=−1000A/s
Using the formula for induced emf in an inductor:
E=−Ldidt
Where:
- L=10H (inductance)
E=−10H×(−1000A/s)=10000V=104V
The average emf induced across the coil is:
Average EMF=104V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION AND REASON
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A12V battery connected ot a 6Ω,10Hcoil through a switch drives a constant current in the ciructit. The switch is suddenly opened. Assuming that it took 1 ms to open the swith, calculate the average emf induced across the coil.
View SolutionIn the circuit, a battery of emf E, a resistance R and inductance coil L1andL2 and switch S are connected as shown. In Fig. Initially the switch is open
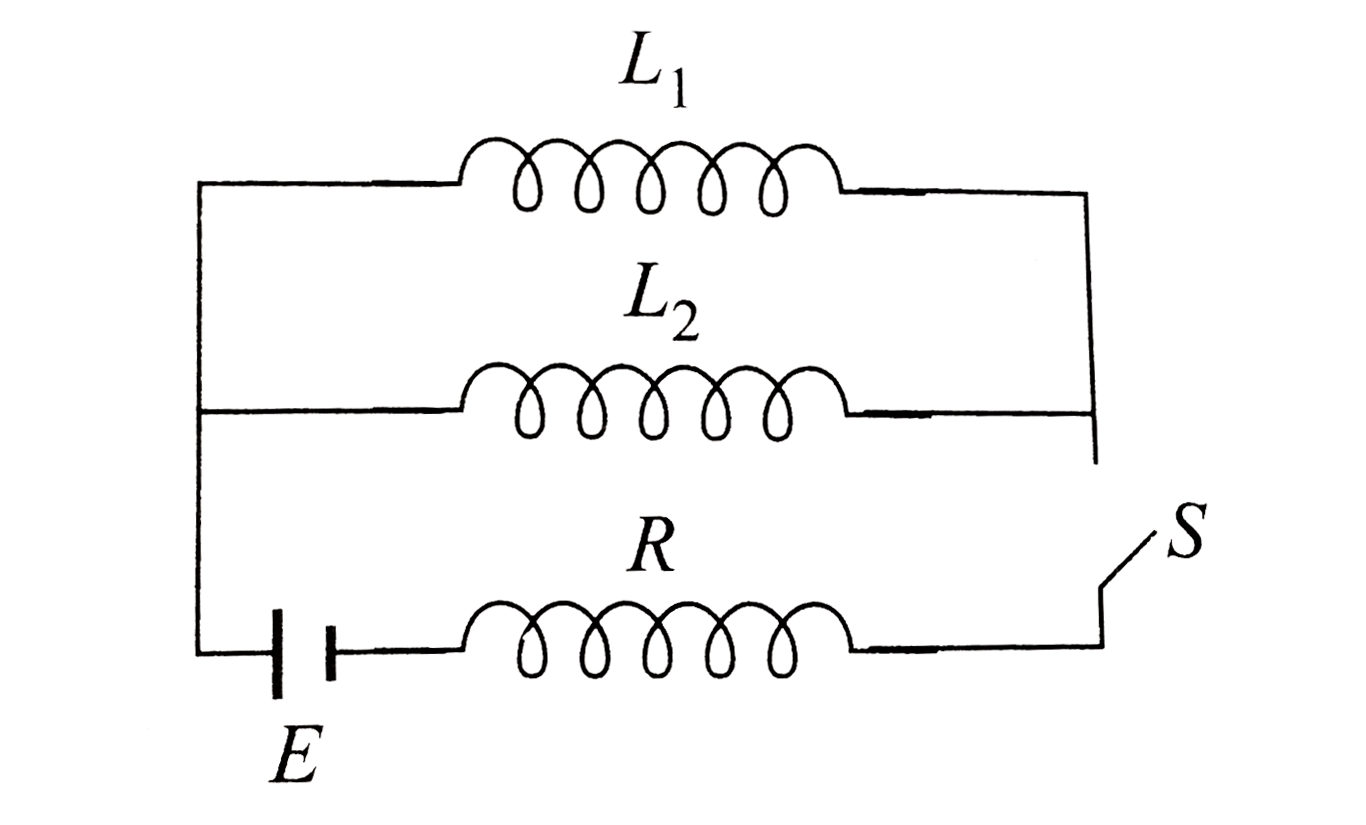
View Solution
Knowledge Check
A battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A2.5Ω,6VB3.5Ω,6VC2.5Ω,7VD3.5Ω,7V
An inductor is connected to a battery through a switch. Explain why the emf induced in the inductor is much larger when the swithc is opened as compared to the emf induced when the switch is closed.
View SolutionA coil of self inductance 10 mH and resistance 0.1 Ω is connected through a switch battery of internal resistance 0.9Ω after the switch is closed, the time taken for the current to attain 80% of the saturation value is [taken ln5=1.6]
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
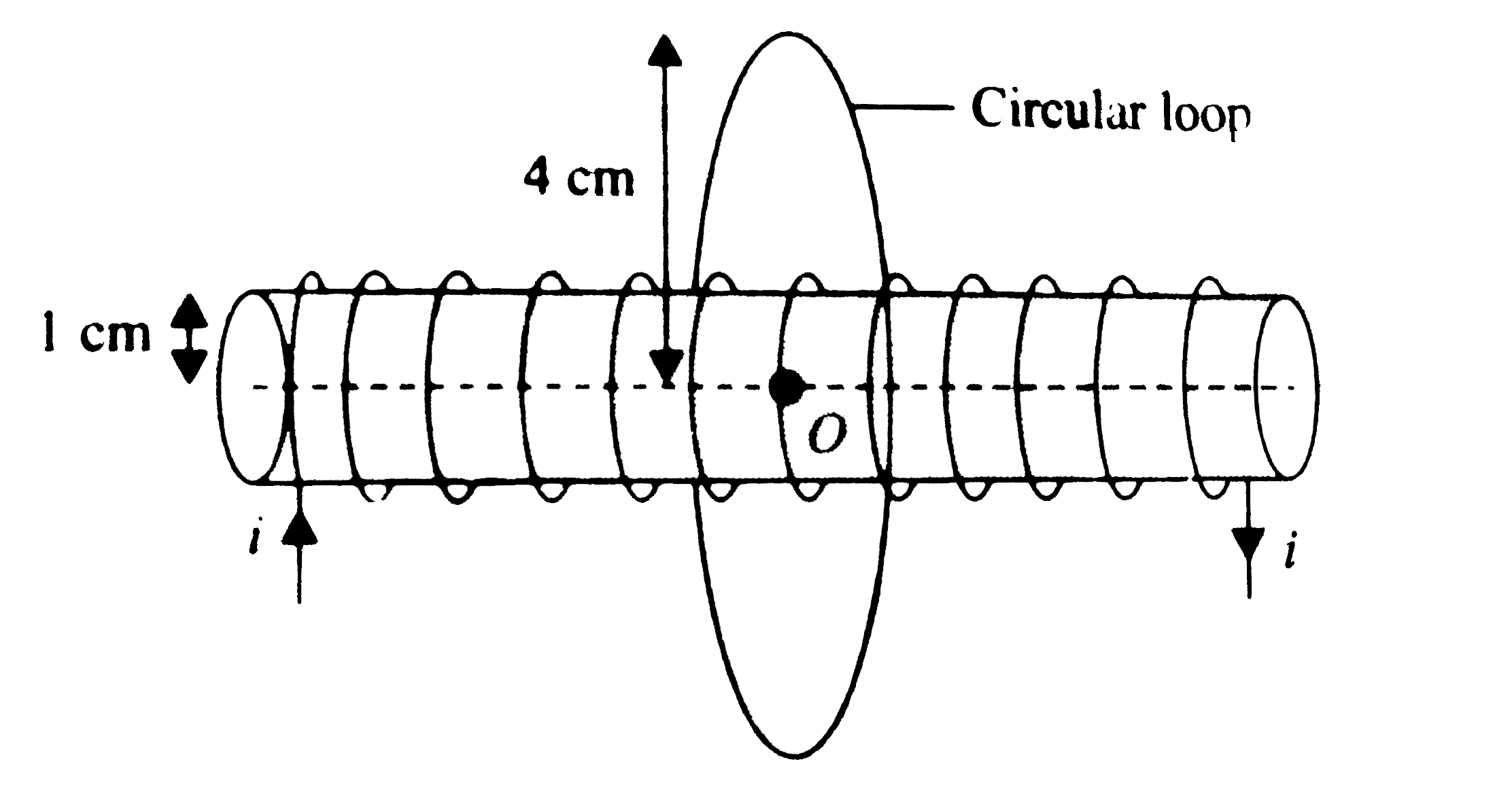
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionA coil of inductance 8.4 mH and resistance 6(Ω) is connected to a 12 V battery. The current in the coil is 1.0 A at approximately the time
View SolutionA coil of inductance 8.4mH and resistance 6 Ω is connected to a 12V battery. The current in the coil is 1.0A at approximately the time.
View SolutionA 1−kΩ resistor is connected in series with a 10−mH inductor, a 30V battery and an open switch. At time t=0, the switch is suddenly closed.
a. What is the maximum current in this circuit and when does it occur?
b. What are the voltage drops across the inductor and across the resistor 20μs after the switch is closed?
c. On a single set of axes, sketch the voltage across the resistor and the voltage across the inductor as functions of time. Also, sketch a graph of the current in the circuit as s function of time.
View Solution
