A 4 A current carrying loop consists of three identical quarter circles of radius 5 cm lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin joined together, value of B at the origin is
μ010(ˆi+ˆj−ˆk)T
μ010(−ˆi+ˆj+ˆk)T
μ05(ˆi+ˆj+ˆk)T
10μ0(ˆi+ˆj+ˆk)T
The correct Answer is:D
To find the magnetic field B at the origin due to a current-carrying loop consisting of three identical quarter circles, we can follow these steps:
Step 1: Understand the Configuration
The loop consists of three quarter circles located in the positive quadrants of the x-y, y-z, and z-x planes. Each quarter circle has a radius of 5 cm (0.05 m), and the current flowing through the loop is 4 A.
Step 2: Determine the Magnetic Field Contribution from Each Quarter Circle
The magnetic field B at the center of a circular loop due to a current I is given by the formula:
B=μ0I4πrθ
where:
- μ0 is the permeability of free space (4π×10−7T m/A),
- r is the radius of the loop,
- θ is the angle subtended at the center (for a quarter circle, θ=π2).
Step 3: Calculate the Magnetic Field for Each Quarter Circle
For each quarter circle, the magnetic field at the origin can be calculated as follows:
1. For the quarter circle in the x-y plane:
Bxy=μ0I4πr⋅π2^k
Substituting I=4A and r=0.05m:
Bxy=(4π×10−7)⋅44π⋅0.05⋅π2^k
2. For the quarter circle in the y-z plane:
Byz=μ0I4πr⋅π2^i
3. For the quarter circle in the z-x plane:
Bzx=μ0I4πr⋅π2^j
Step 4: Combine the Magnetic Fields
Now, we can combine the contributions from all three quarter circles:
B=Bxy+Byz+Bzx
Substituting the values we calculated:
B=(μ0I4πr⋅π2^k+μ0I4πr⋅π2^i+μ0I4πr⋅π2^j)
Factoring out the common term:
B=μ0I4πr⋅π2(^i+^j+^k)
Step 5: Substitute the Values
Now substituting I=4A, r=0.05m:
B=(4π×10−7)⋅44π⋅0.05⋅π2(^i+^j+^k)
This simplifies to:
B=(4×10−7)⋅40.2⋅12(^i+^j+^k)
B=(8×10−6)(^i+^j+^k) T
Final Result
Thus, the magnetic field at the origin is:
B=10μ0(^i+^j+^k) T
The loop consists of three quarter circles located in the positive quadrants of the x-y, y-z, and z-x planes. Each quarter circle has a radius of 5 cm (0.05 m), and the current flowing through the loop is 4 A.
The magnetic field B at the center of a circular loop due to a current I is given by the formula:
B=μ0I4πrθ
where:
- μ0 is the permeability of free space (4π×10−7T m/A),
- r is the radius of the loop,
- θ is the angle subtended at the center (for a quarter circle, θ=π2).
For each quarter circle, the magnetic field at the origin can be calculated as follows:
Bxy=μ0I4πr⋅π2^k
Substituting I=4A and r=0.05m:
Bxy=(4π×10−7)⋅44π⋅0.05⋅π2^k
Byz=μ0I4πr⋅π2^i
Bzx=μ0I4πr⋅π2^j
Now, we can combine the contributions from all three quarter circles:
B=Bxy+Byz+Bzx
Substituting the values we calculated:
B=(μ0I4πr⋅π2^k+μ0I4πr⋅π2^i+μ0I4πr⋅π2^j)
Factoring out the common term:
B=μ0I4πr⋅π2(^i+^j+^k)
Now substituting I=4A, r=0.05m:
B=(4π×10−7)⋅44π⋅0.05⋅π2(^i+^j+^k)
This simplifies to:
B=(4×10−7)⋅40.2⋅12(^i+^j+^k)
B=(8×10−6)(^i+^j+^k) T
Thus, the magnetic field at the origin is:
B=10μ0(^i+^j+^k) T
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude to →B at the origin.
View SolutionA current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. If the current in the loop is i, the resultant magnetic field due to two semicircular parts at their common centre is
View Solution
Knowledge Check
- Question 1 - Select One
A current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with x>0 is now bent so that it now lies in the y-z plane.
AThe magnitude of magnetic moment now diminishes.BThe magnetic moment does not change.CThe magnitude of →B at (0,0,z),z>>R increases.DThe magnitude of →B at (0,0,z),z>>R is unchanged.
A uniform surface charge of density σ is given to a quarter of a disc extending upto infinity in the first quadrant of x-y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the points (0,0,d) & (0,0,2d).
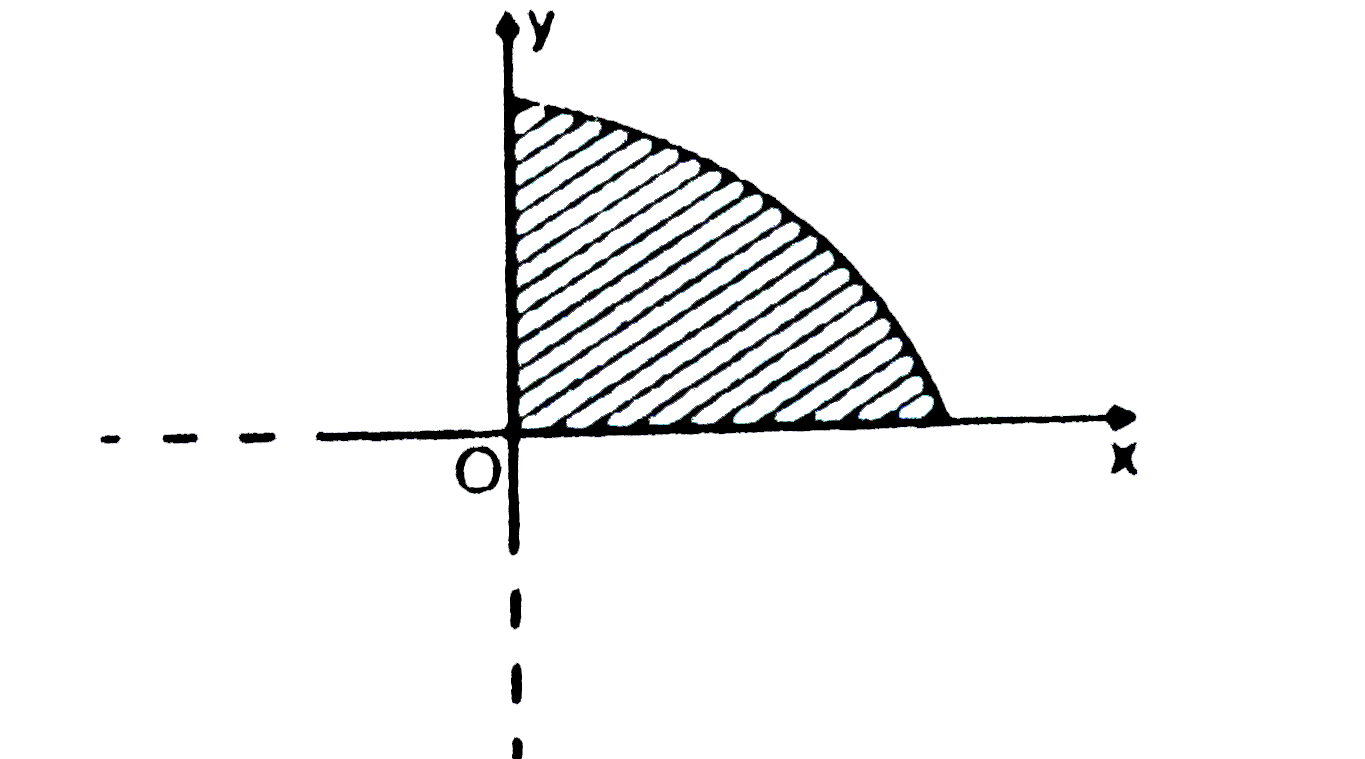 View Solution
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending up to infinity in the first quadrant of x−y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the point (0,0,d) and (0,0,2d)
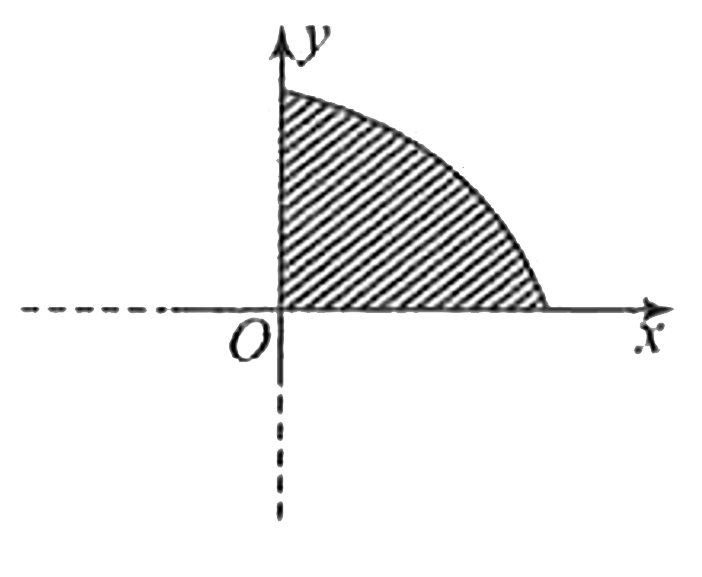 View Solution
View SolutionThe radius of the larger circle lying in the first quadrant and touching the line 4x+3y−12=0 and the coordinate axes, is
View SolutionFind the equation of the circle whose radius is 5 and centre lies on the positive side of x-axis at a distance 5 from the origin.
View SolutionA current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with x>0 is now bent so that it now lies in the y-z plane.
View SolutionAn equation of a plane parallel to the plane x−2y+2z−5=0 and at a unit distance from the origin is
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View Solution
