A system consists of two charges 4μCand−3μC with no external field placed at (−5cm,0,0)and(+5cm,0,0) respectively. The amount of work required to separated the two charges infinitely away from each other is
−1.1J
2J
2.5J
3J
The correct Answer is:A
To find the amount of work required to separate the two charges infinitely away from each other, we can use the formula for the potential energy (U) of a system of two point charges:
U=14πϵ0Q1Q2R
Where:
- U is the potential energy,
- Q1 and Q2 are the magnitudes of the two charges,
- R is the distance between the charges,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
Step 1: Identify the charges and their positions
The charges are given as:
- Q1=4μC=4×10−6C located at (−5cm,0,0)
- Q2=−3μC=−3×10−6C located at (5cm,0,0)
Step 2: Calculate the distance between the charges
The distance R between the two charges can be calculated as:
R=|x2−x1|=|5cm−(−5cm)|=|5+5|=10cm=0.1m
Step 3: Substitute the values into the potential energy formula
Now, substituting the values into the formula for potential energy:
U=14πϵ0Q1Q2R
Using ϵ0≈8.85×10−12C2/N m2:
U=14π(8.85×10−12)(4×10−6)(−3×10−6)0.1
Step 4: Calculate the numerical value
Calculating the numerator:
Q1Q2=(4×10−6)(−3×10−6)=−12×10−12C2
Now substituting into the potential energy formula:
U=14π(8.85×10−12)−12×10−120.1
Calculating the denominator:
4π(8.85×10−12)≈1.112×10−10
Thus,
U=−12×10−121.112×10−10×0.1=−12×10−121.112×10−11≈−1.08J
Step 5: Final answer
The amount of work required to separate the two charges infinitely away from each other is approximately:
U≈−1.08J≈−1.1J
Conclusion
The answer to the question is:
Option A: −1.1J
- U is the potential energy,
- Q1 and Q2 are the magnitudes of the two charges,
- R is the distance between the charges,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
The charges are given as:
- Q1=4μC=4×10−6C located at (−5cm,0,0)
- Q2=−3μC=−3×10−6C located at (5cm,0,0)
The distance R between the two charges can be calculated as:
R=|x2−x1|=|5cm−(−5cm)|=|5+5|=10cm=0.1m
Now, substituting the values into the formula for potential energy:
U=14πϵ0Q1Q2R
Using ϵ0≈8.85×10−12C2/N m2:
U=14π(8.85×10−12)(4×10−6)(−3×10−6)0.1
Calculating the numerator:
Q1Q2=(4×10−6)(−3×10−6)=−12×10−12C2
Now substituting into the potential energy formula:
U=14π(8.85×10−12)−12×10−120.1
Calculating the denominator:
4π(8.85×10−12)≈1.112×10−10
Thus,
U=−12×10−121.112×10−10×0.1=−12×10−121.112×10−11≈−1.08J
The amount of work required to separate the two charges infinitely away from each other is approximately:
U≈−1.08J≈−1.1J
The answer to the question is:
Option A: −1.1J
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
(a) Determine the electrostatic potential energy of a system consisting of two charge 7μCand−2μC (and with no external field) placed at (−9cm,0,0)and(9cm,0,0) respectively.
(b) How much work is required to seperate the two charges infinitely away from each other ?
(c) Suppose that the same system of charges is now placed in an external electric field E=A×1/r2, where A=9×105Cm−2.
What would the electrostatic energy of the configuration be ?
View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).
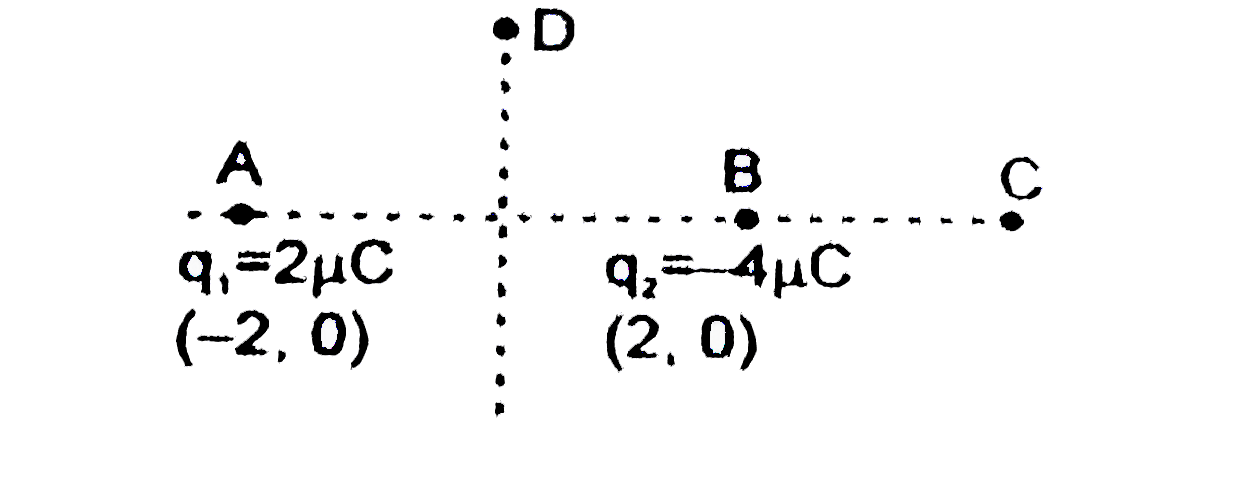
View SolutionTwo point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
View SolutionTwo spheres A and B of radius 4 cm and 6 cm are given charges of 80μCand40μC, respectively. If they are connected by a fine wire, then the amount of charge flowing from one to the other is
View SolutionA charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
View SolutionTwo Charges 5 μC and 20 μC are placed on two concentric circes of radius 10 cm and 20 cm respectively lying in x-y plane . The potential at centre is
View SolutionTwo charges +10μC and +20μC are placed at a. separation of 2 cm. Find the electric potential due to the. pair at the middle point of the line joining the two charges.
View SolutionTwo point charges qA=3μCandqB=−3μC are located 20cm apart in vacuum. What is the electric field at the mid point of the line joining the two charges.
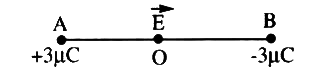
View SolutionFour equal point charges Q each are placed in the xy plane at (0,2), (4,2), (4,-2) and (0, -2). The work required to put a fifth charge Q at the origin of the coordinate system will be
View Solutiontwo point charges + 16 q and -4q located at x=0 and x=L respectively. the location of a point on the x-axis from x=0, at which the net electric field due to these two charges is zero is
View Solution
