Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density p. Assume the velocity is along x-axis and the are of cross-section of the block perpendicular to v0 is A. show that the drag force on the block is 4rAv0√kTm where,m is the mass of the gas molecule.
4pAv0√kTm
2pAv0√kT3m
pA2v0√kTm
v0pA√kT2m
The correct Answer is:A
To derive the expression for the drag force on a rectangular block of wood moving through a gas, we can follow these steps:
Step 1: Understand the System
We have a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. The area of cross-section of the block perpendicular to the velocity is A.
Step 2: Determine the Number Density of Gas Molecules
The number density n of gas molecules can be expressed as:
n=ρm
where m is the mass of a gas molecule.
Step 3: Calculate the Average Speed of Gas Molecules
The average speed v of gas molecules can be derived from the kinetic theory of gases:
v=√8kTπm
where k is the Boltzmann constant.
Step 4: Calculate the Rate of Collisions
The number of collisions per unit time N that the block experiences can be calculated as:
N=n⋅A⋅v
Substituting for n:
N=(ρm)A⋅v
Step 5: Determine the Change in Momentum
When the block moves through the gas, it collides with the gas molecules. The change in momentum during each collision can be considered. For a single molecule, the change in momentum when it collides with the block is:
Δp=2mv
Thus, the total change in momentum per unit time (which gives us the drag force Fd) is:
Fd=N⋅Δp=N⋅2mv
Substituting for N:
Fd=(ρm)Av⋅2mv=2ρAv2
Step 6: Substitute the Average Speed
Now substituting the expression for v:
Fd=2ρA(√8kTπm)2
This simplifies to:
Fd=2ρA⋅8kTπm=16ρAkTπm
Step 7: Relate Density to the Drag Force
Using the ideal gas law, we can relate the density ρ to the number density n and the temperature T:
ρ=nm
Substituting this back into the drag force equation gives:
Fd=16nmAkTπm=16nAkTπ
Step 8: Final Expression for Drag Force
Now, we can express the drag force in terms of the velocity v0:
Fd=4⋅A⋅v0⋅√8kTπm=4Av0√kTm
Thus, we arrive at the final expression for the drag force:
Fd=4Av0√kTm
Final Result
The drag force on the block is given by:
Fd=4Av0√kTm
We have a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. The area of cross-section of the block perpendicular to the velocity is A.
The number density n of gas molecules can be expressed as:
n=ρm
where m is the mass of a gas molecule.
The average speed v of gas molecules can be derived from the kinetic theory of gases:
v=√8kTπm
where k is the Boltzmann constant.
The number of collisions per unit time N that the block experiences can be calculated as:
N=n⋅A⋅v
Substituting for n:
N=(ρm)A⋅v
When the block moves through the gas, it collides with the gas molecules. The change in momentum during each collision can be considered. For a single molecule, the change in momentum when it collides with the block is:
Δp=2mv
Thus, the total change in momentum per unit time (which gives us the drag force Fd) is:
Fd=N⋅Δp=N⋅2mv
Substituting for N:
Fd=(ρm)Av⋅2mv=2ρAv2
Now substituting the expression for v:
Fd=2ρA(√8kTπm)2
This simplifies to:
Fd=2ρA⋅8kTπm=16ρAkTπm
Using the ideal gas law, we can relate the density ρ to the number density n and the temperature T:
ρ=nm
Substituting this back into the drag force equation gives:
Fd=16nmAkTπm=16nAkTπ
Now, we can express the drag force in terms of the velocity v0:
Fd=4⋅A⋅v0⋅√8kTπm=4Av0√kTm
Fd=4Av0√kTm
The drag force on the block is given by:
Fd=4Av0√kTm
Topper's Solved these Questions
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXEMPLAR PROBLEMS
8 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - ASSERTION & REASON
10 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - SPECIFIC CEAT CAPACITY
13 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion And Reason
15 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
15 Videos
Similar Questions
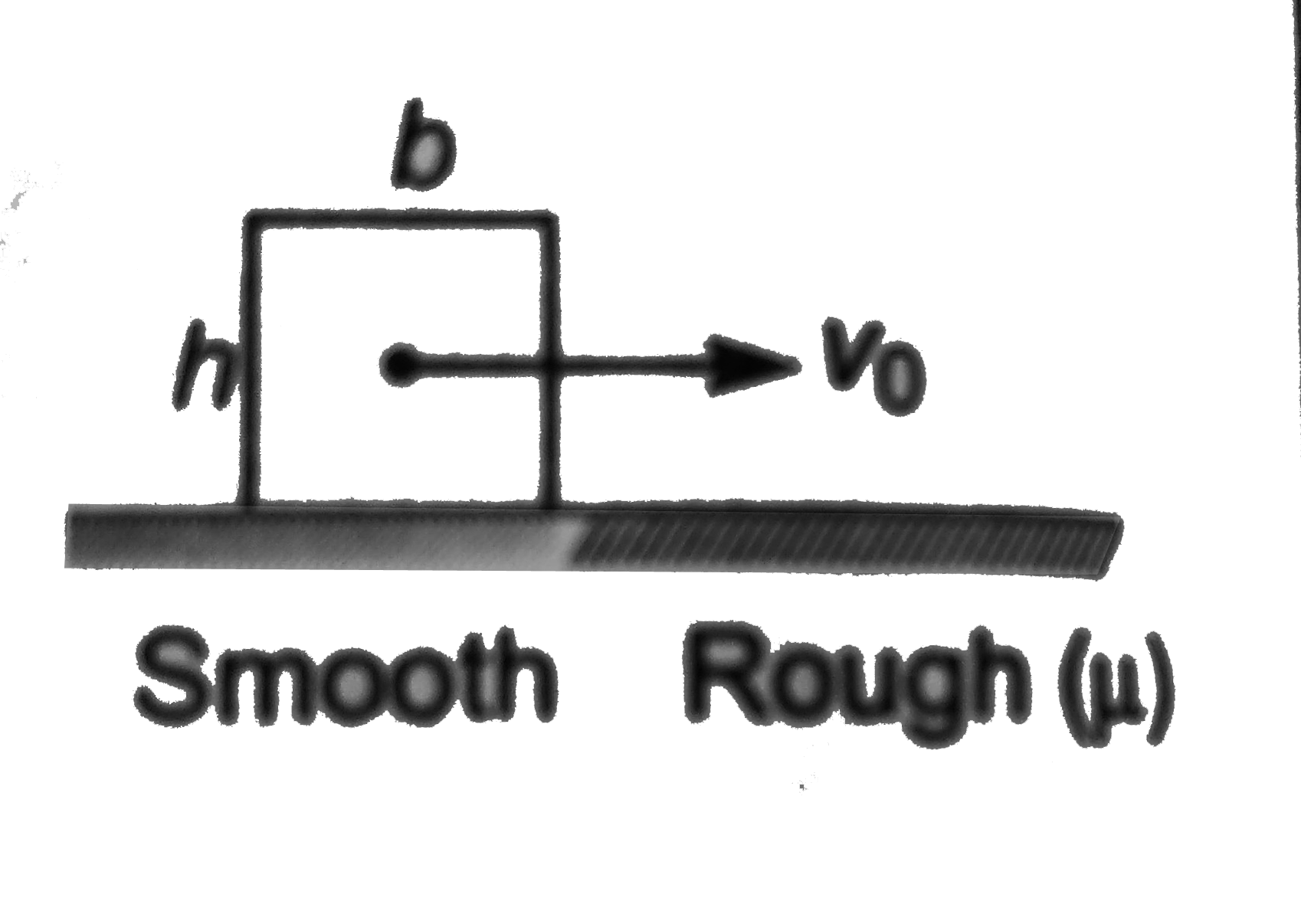
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass 2 kg is moving with a velocity of 2ˆi−ˆj+3ˆk m/s. Find the magnitude and direction of momentum of the block with the x-axis.
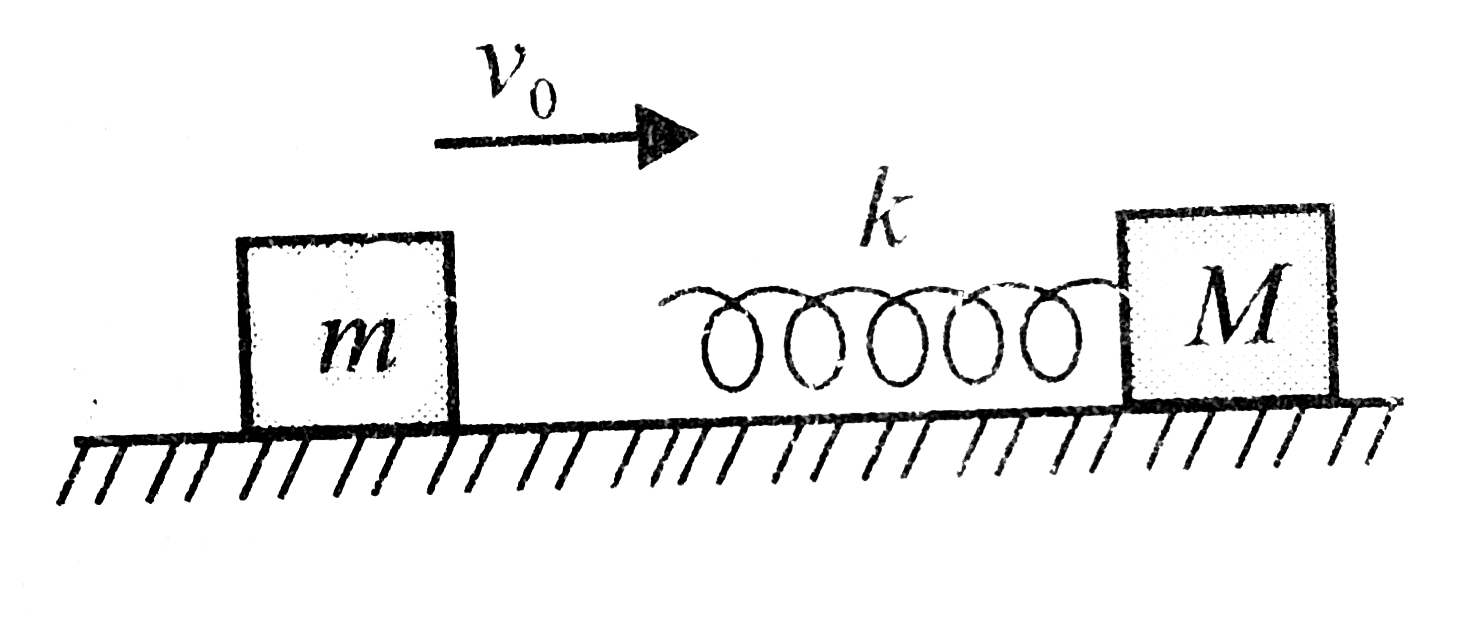
View SolutionA block of mass m moving with a velocity v0 collides with a stationary block of mass M to which a spring of stiffness k is attached, as shown in Fig. Choose the correct alternative(s)
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
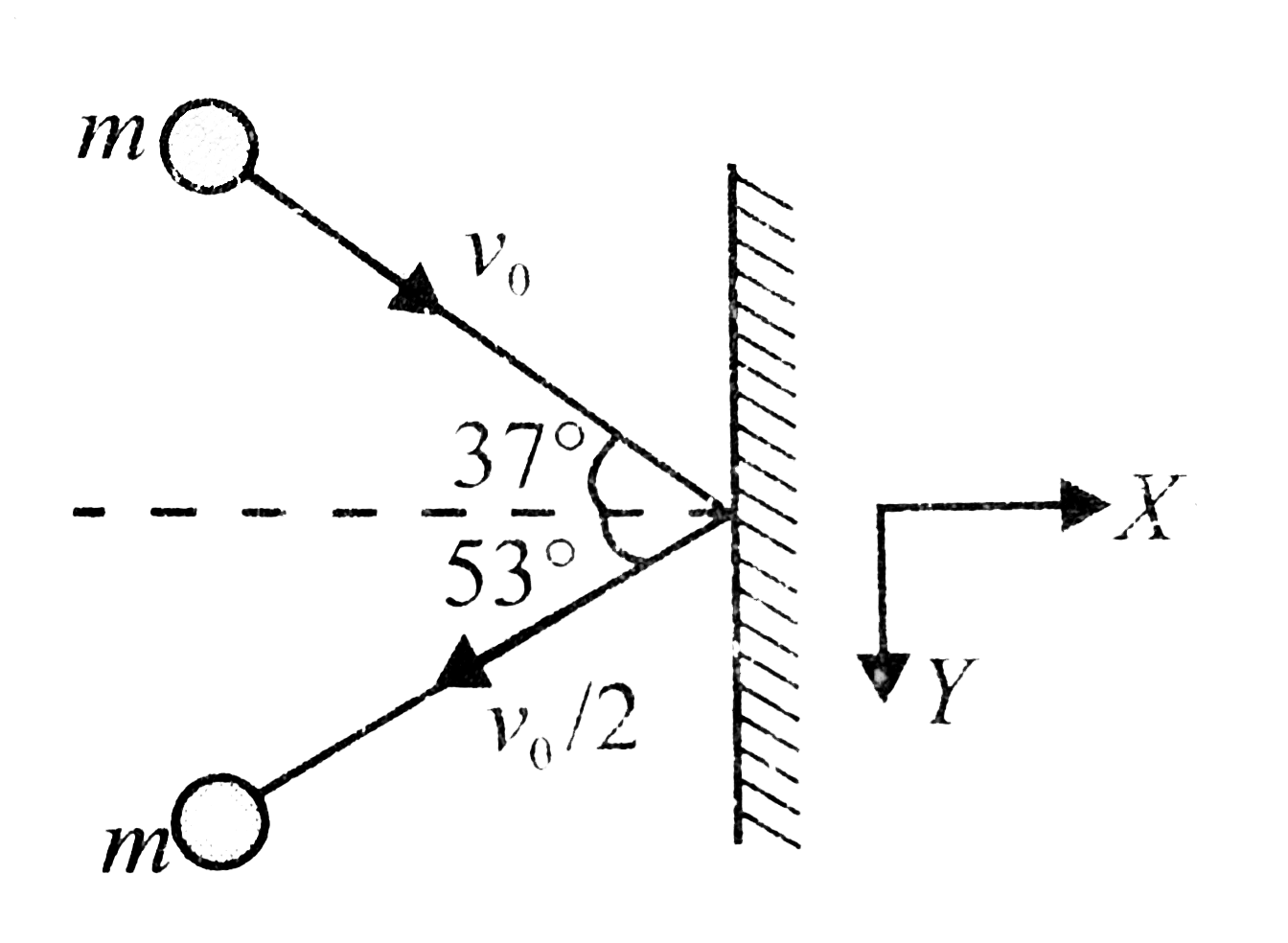
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

View Solution
