The radii of the two columne is U-tube are r1 and r2(>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)
ρghr1r22(r2−r1)
ρgh(r1−r2)2r1r2
2(r2−r1)ρghr1r2
ρgh2(r2−r1)
The correct Answer is:A
To solve the problem, we will derive the expression for the surface tension of the liquid in the U-tube based on the given parameters. Here’s a step-by-step solution:
Step 1: Understand the pressure balance
In a U-tube, the pressure at the same horizontal level in both arms must be equal. Therefore, we can set up the pressure balance equation at the level of the liquid in both arms.
Step 2: Write the pressure equations
Let P1 be the pressure at the level in the left arm and P2 be the pressure at the level in the right arm. The pressures can be expressed as:
- For the left arm:
P1=P0−2Tr1+ρgh
- For the right arm:
P2=P0−2Tr2
Step 3: Set the pressures equal
Since the pressures at the same level must be equal:
P1=P2
Substituting the expressions from Step 2:
P0−2Tr1+ρgh=P0−2Tr2
Step 4: Simplify the equation
Cancel P0 from both sides:
−2Tr1+ρgh=−2Tr2
Rearranging gives:
ρgh=2Tr2−2Tr1
Factoring out 2T:
ρgh=2T(1r2−1r1)
Step 5: Solve for surface tension T
Now, we can isolate T:
T=ρgh2(1r2−1r1)
This can be rewritten as:
T=ρgh⋅r1r22(r2−r1)
Final Expression
Thus, the expression for the surface tension T is:
T=ρghr1r22(r2−r1)
In a U-tube, the pressure at the same horizontal level in both arms must be equal. Therefore, we can set up the pressure balance equation at the level of the liquid in both arms.
Let P1 be the pressure at the level in the left arm and P2 be the pressure at the level in the right arm. The pressures can be expressed as:
- For the left arm:
P1=P0−2Tr1+ρgh
- For the right arm:
P2=P0−2Tr2
Since the pressures at the same level must be equal:
P1=P2
Substituting the expressions from Step 2:
P0−2Tr1+ρgh=P0−2Tr2
Cancel P0 from both sides:
−2Tr1+ρgh=−2Tr2
Rearranging gives:
ρgh=2Tr2−2Tr1
Factoring out 2T:
ρgh=2T(1r2−1r1)
Now, we can isolate T:
T=ρgh2(1r2−1r1)
This can be rewritten as:
T=ρgh⋅r1r22(r2−r1)
Thus, the expression for the surface tension T is:
T=ρghr1r22(r2−r1)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Higher Order Thinking Skills
8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Exemplar Problems
5 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The radii of the two columns is U-tube are r1 and r2(r2>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)
View SolutionIn a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -
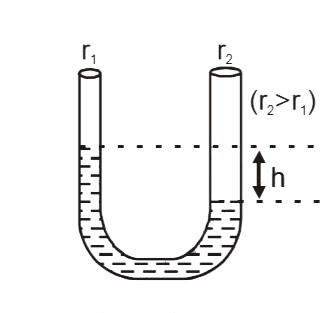
View Solution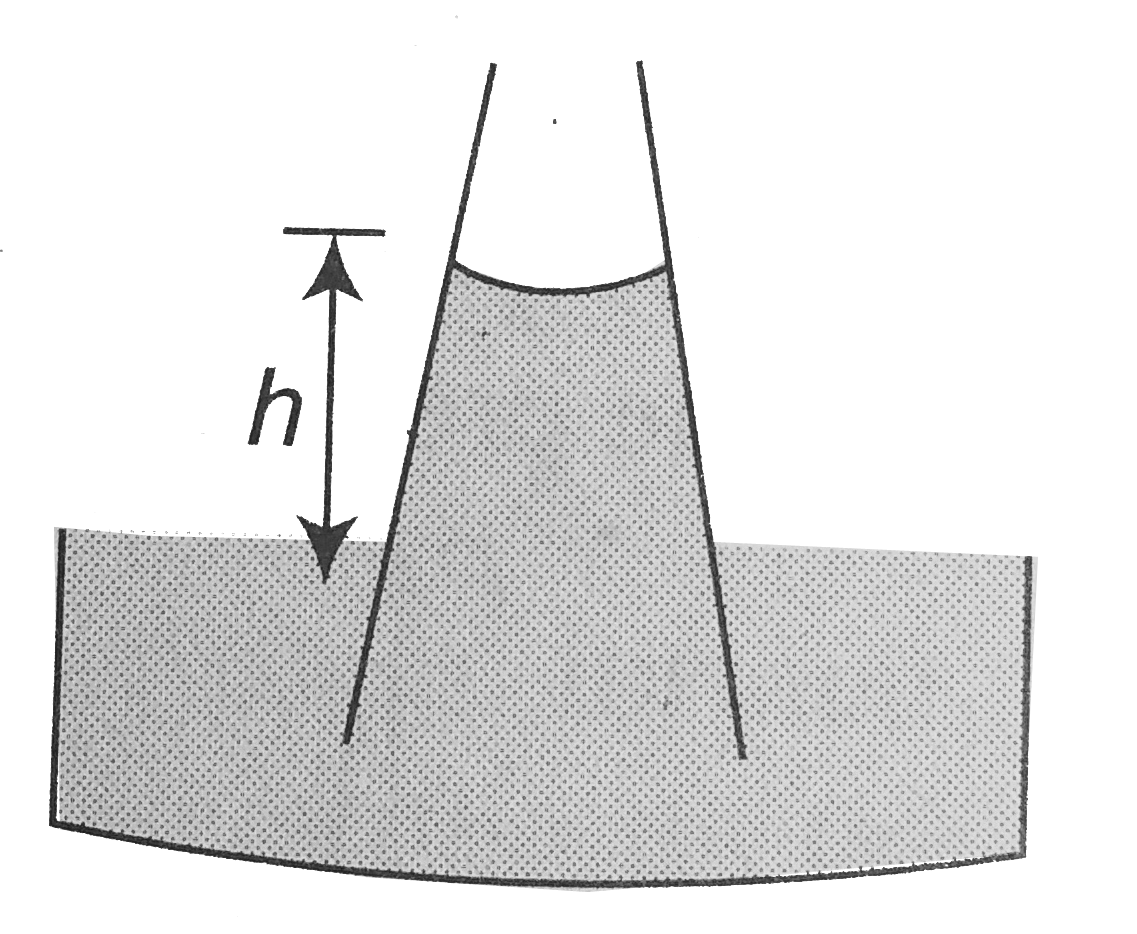
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
What is the potential energy acquired by the liquid in the capillary?
View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

If density of lower liquid is increased
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View SolutionWhat is the height to which a liquid rises between two long parallel plates, a distance d apart ? (Surface tension of liquid is T and density is ρ)
View SolutionWhen a vertical capillary of length with the sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature this process remains constant.)

View SolutionWhen a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature in this process remains constant.)

View Solution
