अंतराल [1,e] में x2logx का महत्तम मान है
e2
1elog1√e
e2log√e
इनमे से कोई नहीं
The correct Answer is:A
Step by step video, text & image solution for अंतराल [1,e] में x^(2)logx का महत्तम मान है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- अवकलन तथा अवकलज के अनुप्रयोगBOOK - ERRORLESS HINDICHAPTER - अवकलन तथा अवकलज के अनुप्रयोगEXERCISE - MULTIPLE CHOICE QUESTIONS (एक बिन्दु पर अवकलज,मानक अवकलज)
186 Videos
- अवकलन तथा अवकलज के अनुप्रयोगBOOK - ERRORLESS HINDICHAPTER - अवकलन तथा अवकलज के अनुप्रयोगEXERCISE - MULTIPLE CHOICE QUESTIONS (अस्पष्ट फलनों का अवकलन,प्रचलिक व संयुक्त फलनों का अवकलन,लघुगणकीय अवकलन, अनन्त श्रेणियों के अवकलन )
64 Videos
- अवकल समीकरण BOOK - ERRORLESS HINDICHAPTER - अवकल समीकरण EXERCISE - JEE Advanced ( Matrix Match type questions )
3 Videos
- केन्द्रीय प्रवृत्ति के मापBOOK - ERRORLESS HINDICHAPTER - केन्द्रीय प्रवृत्ति के मापEXERCISE - Jee Advanced (Reasoning )
2 Videos
Similar Questions
2f(x)=f'(x) एवं f(0)=3, तब f(2)=
View Solutionमाना y,x2x−2xxcoty−1=0 से परिभाषित x का एक अस्पष्ट फलन है। तब y'(1) बराबर है
View Solution
View Solutionकथन - 1 : प्रथम n सम धन पूर्णांकों का प्रसरण n2−14 है।
कथन - 2 : प्रथम n धन पूर्णाको का योगफल n(n+1)2 और प्रथम n धन पूर्णांको के वर्गों का योगफल n(n+1)(2n+1)6 है।
View Solutionनिम्न में से समाकलन ∫cos2x dx का सही मान है -
View Solutionयदि limx→alogx−logax−a+klimx→elogx−1x−e=1 तो k का मान है -
View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
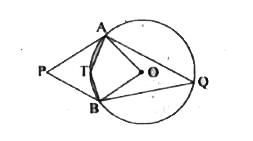
View Solutiona का न्यूनतम मान ज्ञात कीजिए कि फलन f(x)=x2+ax+5 अंतराल [1, 2] में वर्धमान है।
View Solution352 का मान है-
View Solutionसिद्ध कीजिए f(x)=x2 अंतराल (0,∞) में वर्धमान तथा अंतराल (−∞,0) में हस्यमान है।
View Solutionफलन x2logx अन्तराल (1,e) में रखता है
View Solutionफलन logxx का, अन्तराल [2,∞) में न्यूनतम मान होगा
View Solutionअंतराल (0,π2) में फलन log sin x है
View Solutionlimx→ax−1−a−1x−a का मान है
View Solutionlimx→0x|x|+x2 का मान है
View Solutionदिया गया है कि limx→0eax−bx−1x2=2, तब |a|+|b| का मान है
View Solution
