Figure shows the graph of velocity versus displacement of a particle executing simple harmoic motion. Find the period of oscillation of the particle.
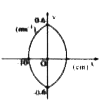
xmax=A=10cm and
vmax=ωA=0.6ms−1
∴ω=vmaxxmax=6×10−110×10−2=6rads−1
∴T=2πω=2π6=π3 sec
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE I
Explore 184 Videos
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE II
Explore 175 Videos
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE-3
Explore 49 Videos
- OSCILLATIONBook:AAKASH SERIESChapter:OSCILLATIONExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 12 Videos
- PHYSICAL WORLDBook:AAKASH SERIESChapter:PHYSICAL WORLDExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
Figure shows the graph of velocity versus displacement of a partciel executing simple harmonic motion. Find the period of oscillation of the particle.

View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-
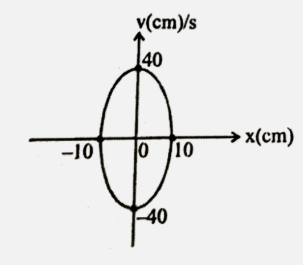
View Solution
Knowledge Check
The velocity of a particle executing simple harmonic motion is
Aω2√A2+x2Bω√A2−x2Cω√A2+x2Dω2√A2−x2The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2πIf a particle is executing simple harmonic motion, then acceleration of particle
Ais uniformBvaries linearly with timeCis non uniformDBoth (2) & (3)
The plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View SolutionThe ratio of the maximum velocity and maximum displacement of a particle executing simple harmonic motion is equal to
View Solution

