
A block lying on a rough horizontal surfaces as show in figure . Its mass is M and it is dispalced through a distance d by a force →F acting at an angle θ with horizontal . If μ is the coefficient of friction between a block and the surface and mass of block is M . then work done is ...........Solution in Gujrati
W=[F(sinθ+μcosθ)−μMg]d
W=[F(cosθ+μsinθ)−μMg]d
W=[Fsinθ+μcosθ)+μMg]d
W=[F(cosθ−μsinθ)+μMg]d
The correct Answer is:B
W=[F(cosθ+μsinθ)−μMg]d
FBD of a block is shown in figure below :

As there is no displacement in Y - direction ,
N+F∈θ=Mg=0
∴N+Fsinθ=Mg
∴N=Mg−Fsinθ......(i)
Force responsible for displacement in X direction ,
F1=Fcosθ−f where , f = frictional force = μN
=Fcoθ−μN
∴F1=Fcosθ−μ(Mg−Fsinθ)
( From eq.(1) ).....(ii)
Now , work W=F1d
=[Fcosθ−μMg+Fμsinθ]d
[ From wq. (2)]
=[Fcosθ+Fμsinθ−μMg]d
∴W=[F(cosθ+μsinθ)−μMg]d
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - F Questions From Module (Sample questions for preparation of competitive exams)
Explore 23 Videos
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:QUESTION PAPER (SECTION - A)
Explore 6 Videos
- WORK, ENERGY AND POWER Book:KUMAR PRAKASHANChapter:WORK, ENERGY AND POWER Exercise:SECTION - D NCERT Exemplar Solutions (Long Answer Type Questions)
Explore 5 Videos
- WAVESBook:KUMAR PRAKASHANChapter:WAVESExercise:SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
Explore 23 Videos
Similar Questions
A Sphere makes an inslastic collision with another sphere of same mass , then both the spheres are moving .The angle between their direction of motion will be ……..
View SolutionWhen force is exerted on a body what is necessary for work done ?
View SolutionA block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30∘ by a force of 10 N parallel to the inclined surface (figure) . The coefficient of friction between block and the incline is 0.1 .If the block is pushed up by 10 m along teh inclined calculate

(a) work done against gravity
(b) work done against force of friction
(c ) increases in potential energy
(d) increases in kinetic energy
(e) work done by applied force
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionA block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
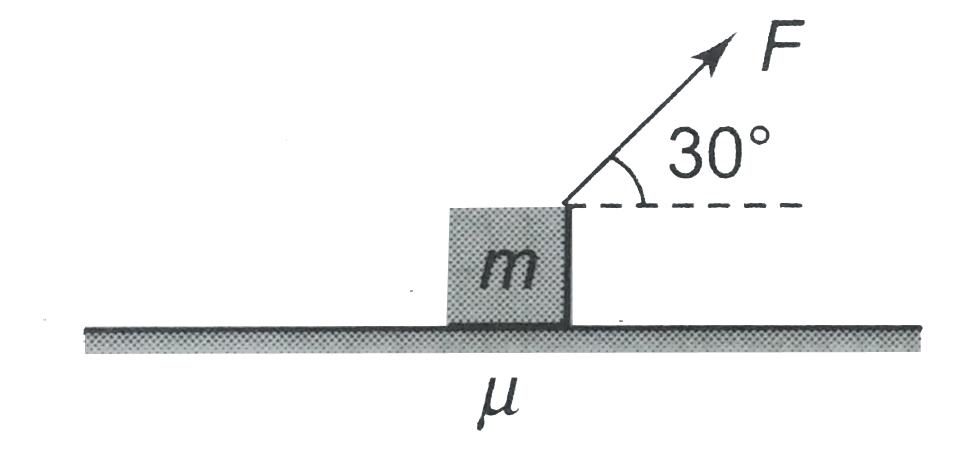
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

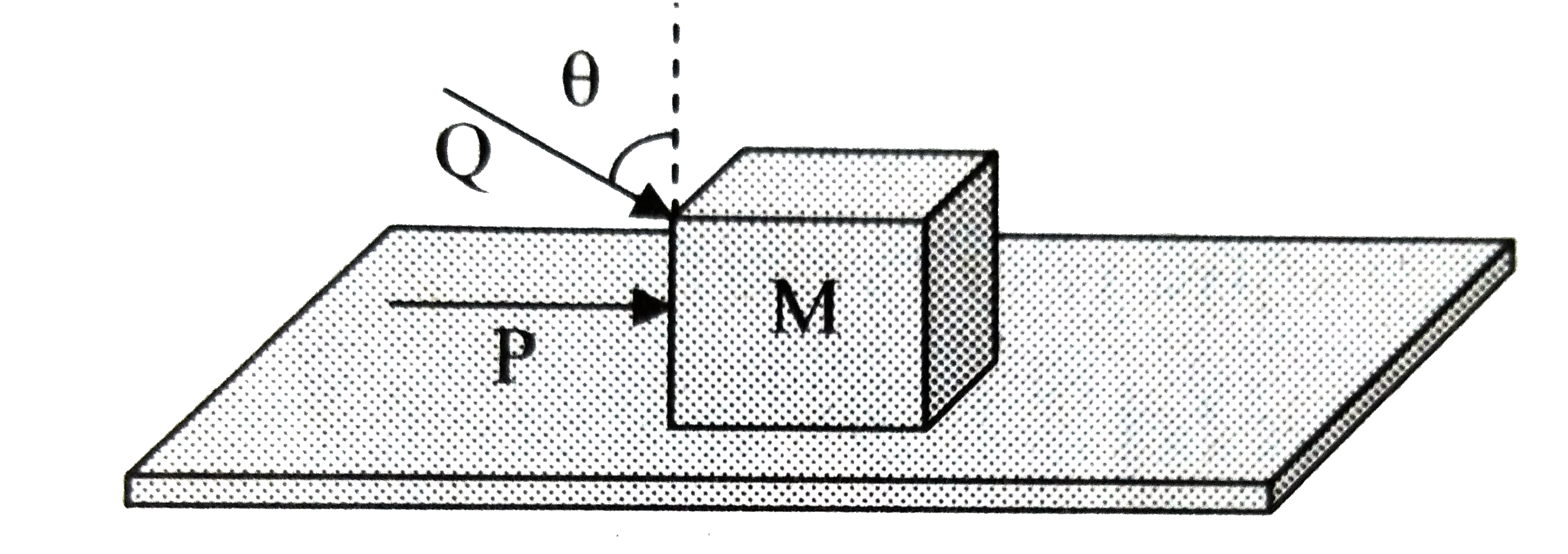
View SolutionA block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction mu. A force is applied to the block at an angle theta with the horizontal. The block will move with a minimum force F if
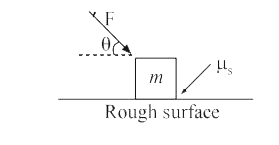
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
View SolutionA block of mass m, lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q, inclined at an angle θ to vertical. The block will remain in equilibrium, if coefficient of friction between it and surface is:
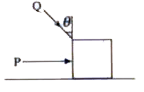
View SolutionA block of mass m, lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q, inclined at an angle θ to vertical. The block will remain in equilibrium, if coefficient of friction between it and surface is

View SolutionA block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is

View SolutionA block of mass m is lying on horizontal surface of coefficient of friction mu. A force is applied to the block at an angle theta with the horizontal. The block will move with a minimum force F if
View Solutionचित्रानुसार खुरदरी क्षैतिज सतह पर ब्लॉक A को ठीक फिसलने के लिए ब्लॉक B का न्यूनतम द्रव्यमान (रस्सी तथा क्षैतिज से किसी विशेष कोण θ पर ) m2 है। यदि धरातल तथा ब्लॉक A के मध्य घर्षण गुणांक μ है तो का मान होगा।
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?

View Solution

