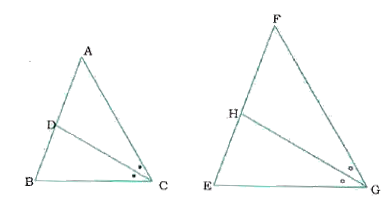
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
CDGH=ACFG
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:CDGH=ACFG
Step by step video, text & image solution for CD and GH are respectively the bisectors of /_ACB" and "/_EGF such that D and H lie on sides AB and FE of DeltaABC" and "DeltaEFG respectively. If DeltaABC ~ DeltaFEG, show that : (CD)/(GH)=(AC)/(FG) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:EXERCISE 6.4
Explore 9 Videos
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:EXERCISE 6.5
Explore 23 Videos
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:EXERCISE 6.2
Explore 12 Videos
- SURFACE AREAS AND VOLUMESBook:KUMAR PRAKASHANChapter:SURFACE AREAS AND VOLUMESExercise:TEST YOUR SKILLS
Explore 5 Videos
Similar Questions
Let ΔABC~ΔDEF and their areas be, respectively, 64cm2 and 121cm2. If EF=15.4cm, find BC.
View SolutionSides of triangles are given below, Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse :
7 cm, 24 cm, 25 cm
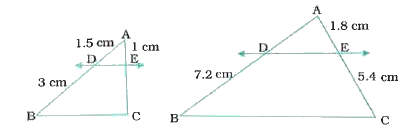
View SolutionIn the given figures 1 and 2, DE∣∣BC. Find the EC in 1 and AD in 2.
View SolutionThe slant height of a frustum of a cone is 4 m and the perimeter of circular ends are 18 m and 16 m. Find the cost of painting its curved surface at 10 per sq. m.
View Solution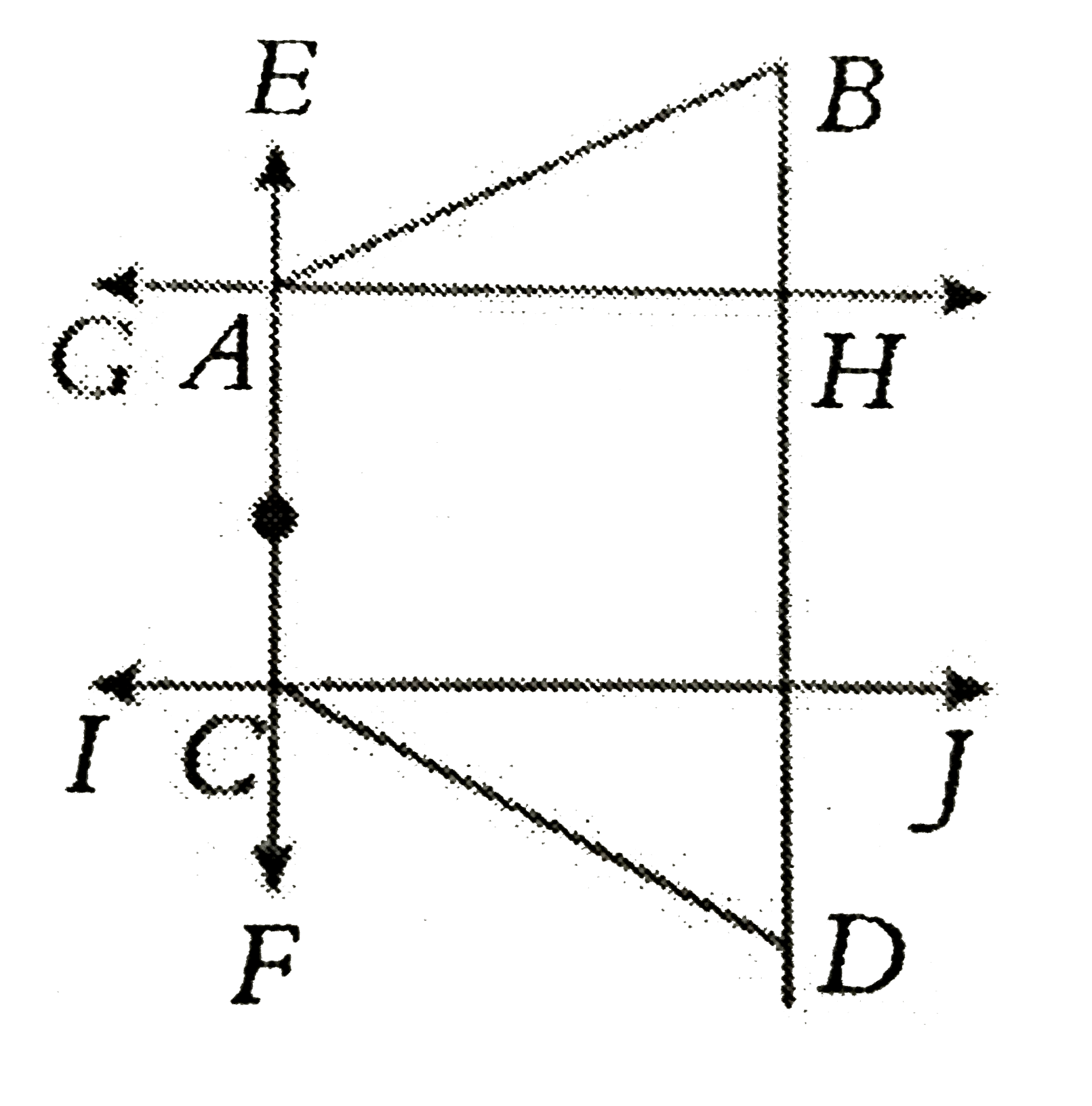
In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCB~ΔHGE
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF
View Solution

