Draw a plot of spring force Fs and displacement x. Hence find an expresion for the P.E. of an elatic stretched spring,
To solve the question, we will follow these steps:
Step 1: Understand Hooke's Law
The spring force Fs is given by Hooke's Law, which states that the force exerted by a spring is directly proportional to the displacement x from its equilibrium position. Mathematically, this is represented as:
Fs=−kx
where k is the spring constant, and x is the displacement from the equilibrium position.
Step 2: Draw the Plot of Spring Force vs. Displacement
1. Axes: Draw a graph with the horizontal axis representing displacement x and the vertical axis representing the spring force Fs.
2. Plotting Points: Since Fs is proportional to x, the graph will be a straight line starting from the origin (0,0) and sloping downwards to the left for negative displacements and upwards to the right for positive displacements.
3. Labeling: Label the slope as k (the spring constant) and indicate the direction of the force (negative for compression and positive for extension).
Step 3: Find the Expression for Potential Energy (P.E.) of a Stretched Spring
The potential energy stored in a spring when it is stretched or compressed is given by the formula:
PE=12kx2
This formula can be derived from the work done on the spring when it is stretched from 0 to x.
Step 4: Derivation of Potential Energy
1. Work Done: The work done on the spring to stretch it from 0 to x is equal to the area under the force vs. displacement graph.
2. Area Calculation: The area under the graph (which is a triangle) can be calculated as:
Area=12×base×height=12×x×Fs
Since Fs=kx, we substitute to get:
Area=12×x×kx=12kx2
3. Conclusion: Thus, the potential energy PE stored in the spring when it is stretched or compressed is:
PE=12kx2
Summary
- We have drawn the plot of spring force Fs against displacement x.
- We derived the expression for the potential energy of an elastic stretched spring as PE=12kx2.
The spring force Fs is given by Hooke's Law, which states that the force exerted by a spring is directly proportional to the displacement x from its equilibrium position. Mathematically, this is represented as:
Fs=−kx
where k is the spring constant, and x is the displacement from the equilibrium position.
1. Axes: Draw a graph with the horizontal axis representing displacement x and the vertical axis representing the spring force Fs.
2. Plotting Points: Since Fs is proportional to x, the graph will be a straight line starting from the origin (0,0) and sloping downwards to the left for negative displacements and upwards to the right for positive displacements.
3. Labeling: Label the slope as k (the spring constant) and indicate the direction of the force (negative for compression and positive for extension).
The potential energy stored in a spring when it is stretched or compressed is given by the formula:
PE=12kx2
This formula can be derived from the work done on the spring when it is stretched from 0 to x.
1. Work Done: The work done on the spring to stretch it from 0 to x is equal to the area under the force vs. displacement graph.
2. Area Calculation: The area under the graph (which is a triangle) can be calculated as:
Area=12×base×height=12×x×Fs
Since Fs=kx, we substitute to get:
Area=12×x×kx=12kx2
3. Conclusion: Thus, the potential energy PE stored in the spring when it is stretched or compressed is:
PE=12kx2
- We have drawn the plot of spring force Fs against displacement x.
- We derived the expression for the potential energy of an elastic stretched spring as PE=12kx2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
There are two springs P and Q . Spring constant for P is K and that for Q is 3K . Both the springs are elongated by applying force of same magnitude . If U is energy stored in spring P then energy stores in spring Q is
A3UBU/3C9UDU/9The elastic potential enegry of a stretched spring is given by E=50x2. Where x is the displacement in meter and and E is in joule, then the force constant of the spring is
A50 NmB100Nm−1C100N/m2D100 NmTwo springs have force constants kA and kB such that kB=2kA. The four ends of the springs are stretched by the same force. If energy stored in spring A is E, then energy stored in spring B is.
AE2B2ECED4E
The force constant between the restoring force F and displacement x of a spring accoring to the graph shown will be
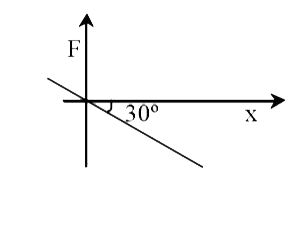
View SolutionA spring of spring constant k is stretched by distance r. Obtain formula for elastic potential energy of a stretched spring. Plot graph of energies versus distance.
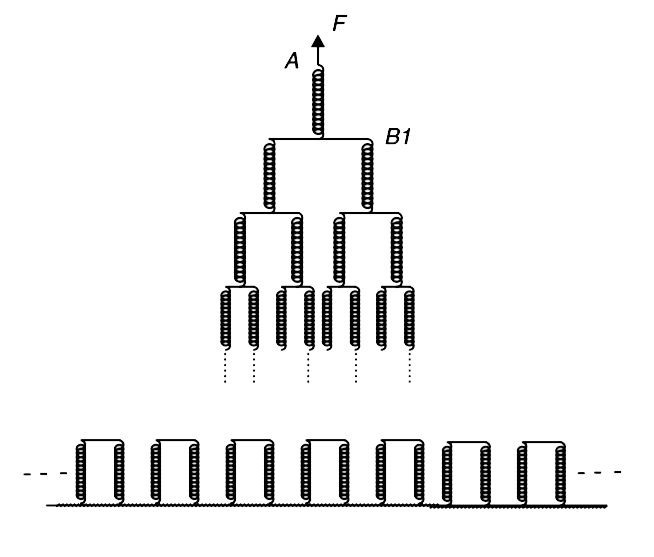
View SolutionThe fig. shows an infinite tower of identical springs each having force constant k. The connecting bars and all springs are massless. All springs are relaxed and the bottom row of springs is fixed to horizontal ground. The free end of the top spring is pulled up with a constant force F. In equilibrium, find
(a) The displacement of free end A of the top spring from relaxed position.
(b) The displacement of the top bar B1 from the initial relaxed position.
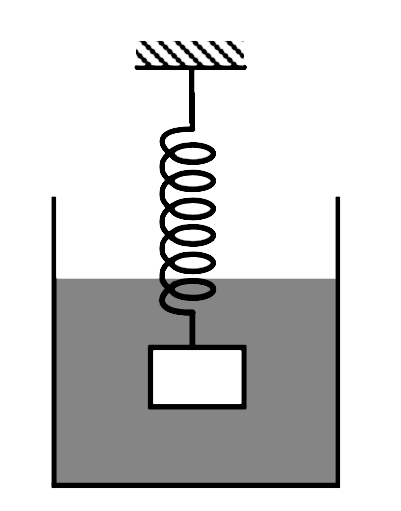
View SolutionAn object with uniform density ρ is attached to a spring that is known to stretch linearly with applied force as shown below.
When the spring-object system is immersed in a liquid of density ρ1 as shown in the figure, the spring stretches by an amount x1(ρ>ρ1). When the experiment is repeated in a liquid of density ρ2>ρ1, the spring stretches by an amount x2. Neglecting any buoyant force on the spring, the density of the object is
View SolutionA block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
View Solution
