If T1,T2 and T3 are the temperatures at which the urms,uaverage,ump of oxygen gas are all equal to 1500 m/s then the correct statement is :
T1>T2>T3
T1<T2<T3
T1=T2=T3
None of these
The correct Answer is:b
To solve the problem, we need to find the temperatures T1,T2, and T3 at which the root mean square speed (urms), average speed (uaverage), and most probable speed (ump) of oxygen gas are all equal to 1500 m/s. We will use the formulas for each of these speeds and derive the corresponding temperatures.
Step 1: Write the formula for urms
The formula for the root mean square speed (urms) is given by:
urms=√3RTM
Where:
- R is the universal gas constant,
- T is the temperature in Kelvin,
- M is the molar mass of the gas.
Given that urms=1500m/s, we can set up the equation:
√3RT1M=1500
Step 2: Solve for T1
Squaring both sides gives:
3RT1M=15002
Rearranging for T1:
T1=15002⋅M3R
Calculating T1:
Assuming R and M are constants, we can compute T1 numerically. Let's say R=8.314J/(mol⋅K) and M for oxygen is approximately 32g/mol=0.032kg/mol:
T1=15002⋅0.0323⋅8.314
Calculating this gives:
T1≈750000K
Step 3: Write the formula for uaverage
The formula for the average speed (uaverage) is given by:
uaverage=√8RTπM
Setting uaverage=1500m/s:
√8RT2πM=1500
Step 4: Solve for T2
Squaring both sides gives:
8RT2πM=15002
Rearranging for T2:
T2=15002⋅πM8R
Calculating T2:
Using the same values for R and M:
T2=15002⋅π⋅0.0328⋅8.314
Calculating this gives:
T2≈883125K
Step 5: Write the formula for ump
The formula for the most probable speed (ump) is given by:
ump=√2RTM
Setting ump=1500m/s:
√2RT3M=1500
Step 6: Solve for T3
Squaring both sides gives:
2RT3M=15002
Rearranging for T3:
T3=15002⋅M2R
Calculating T3:
Using the same values for R and M:
T3=15002⋅0.0322⋅8.314
Calculating this gives:
T3≈1125000K
Step 7: Compare the temperatures
Now we have:
- T1≈750000K
- T2≈883125K
- T3≈1125000K
From this, we can conclude:
T1<T2<T3
Final Answer
The correct statement is T1<T2<T3.
- R is the universal gas constant,
- T is the temperature in Kelvin,
- M is the molar mass of the gas.
- T2≈883125K
- T3≈1125000K
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 230videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 14videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems14videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems1videos
IONIC EEQUILIBRIUM
Similar Questions
Calculate the temperature at which the root mean square velocity, the average velocity, and the most proable velocity of oxygen gas are all equal to 1500ms−1.
View SolutionIf t(u)=au2−3u+1andt(3)=37, what is a?
View SolutionThree projecties are thrown all with same speed u but at different angles of projection (θ>θ2>θ3) all taken from horizontal. Maximum height attained by projectile (3) is H. Range of (1) & (3) is same & that of (2) is maximum for the given speed. At height H, speeds are v1,v2&v3 as shown. Total time of flights are T1,T2&T3. Choose the correct statement(s).
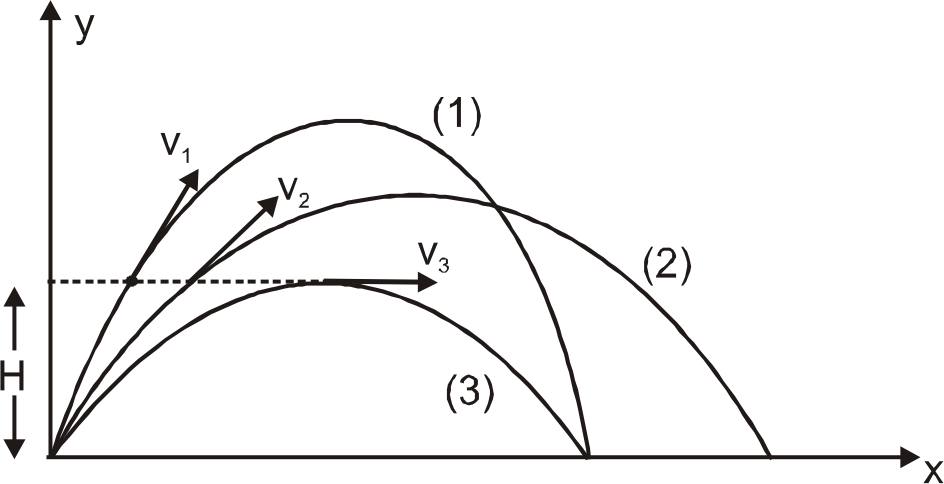 View Solution
View SolutionA body is projected up with a speed u and the time taken by it is T to reach the maximum height H. Pich out the correct statement
View SolutionProve the relation, st=u+at−12a.
View SolutionFor gas at a temperature T the root-mean-square speed vrms, the most probable speed vmp, and the average speed vav obey the relationship
View SolutionAn ideal gas is heated from termperature T1 to T2 under various conditions. The correct statements(s) is/are:-
View SolutionWhat will be the relation between the T1 of gas 1 with M1=56 and T2 of gas 2 with M2=44 if the average speed of gas 1 is equal to most probable speed of gas 2?
View SolutionInternal energy of n moles of helium at temperature T1K is equal to the internal energy of 2n moles of oxygen gas at temperature T2K then the value of T1T2will be
View SolutionTwo stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u1=30m/sec and u2=50m/sec. Which of the curve represent correct variation (for the time interval in which both reach the ground) of
(x2−x1) = the relative position of second stone with respect to first with time (t)
(v2−v1) = the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.View Solution
