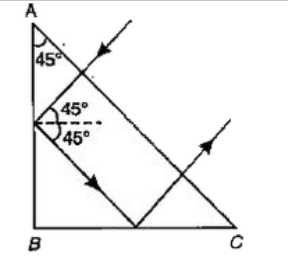
Consider the situation shown in figure. Light from a point source S is made parallel by a convex lens L. The beam travels horizontally and falls on an prism as shown in figure. It passes through the prism symmetrically. The transmitted light falls on a vertical mirror. Through what angle should the mirror be rotated so that an image of S is formed as S itself?

The parallel beam after going through the prism will be deviated by an angle . If the mirror is also rotated by this angle . The rays will fal normally on it. The rays will be reflected back along the same path and form the image of S on itself.
as the prismis thin, the angle is given by
thus , the mirror should be rotated by
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -1
15 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
A horizontal ray of light passes through a prism of index 1.50 and apex angle 4∘ and then strikes a vertical mirror , as shown in the figure. Through what angle must the mirror be rotated if after reflection the ray is to be horizontal?
_E01_041_Q01.png)
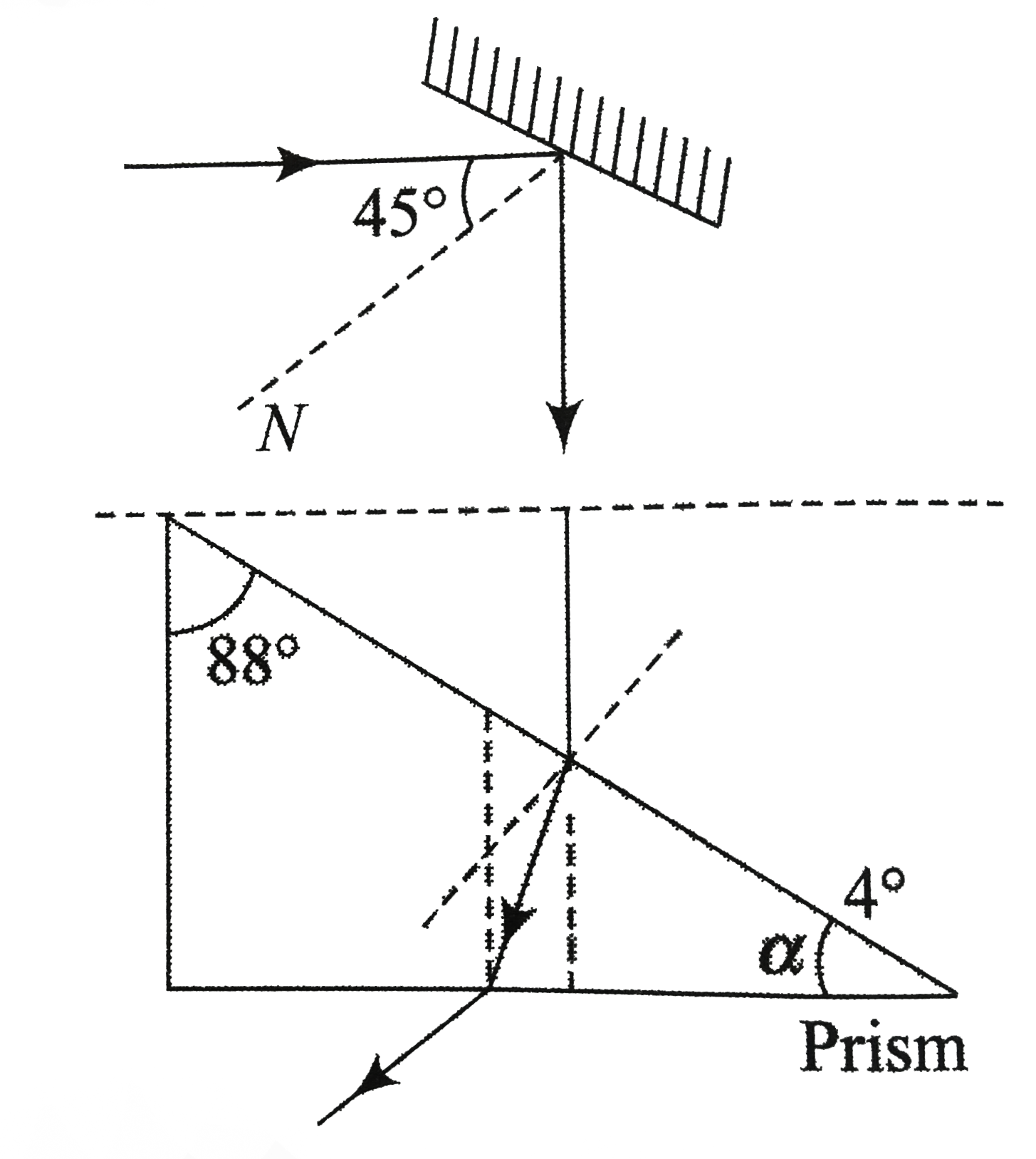
View SolutionA ray of light strikes a plane mirror at an angle of incidence 45∘ as shown in Figure . After reflection,l the ray passes through a prism of refractive indes 1.5 whos apex angle is 4∘. Through what angle must the mirror be rotated it total deviation of the ray be 90∘ ?
View SolutionA horizontal light ray passes through a prism (μ=1.5) of angle 4∘.Further, it is incident on a plane mirror M, that has been placed verticall. By what angle the mirror is rotated so that the ray after reflection becomes horizontal?
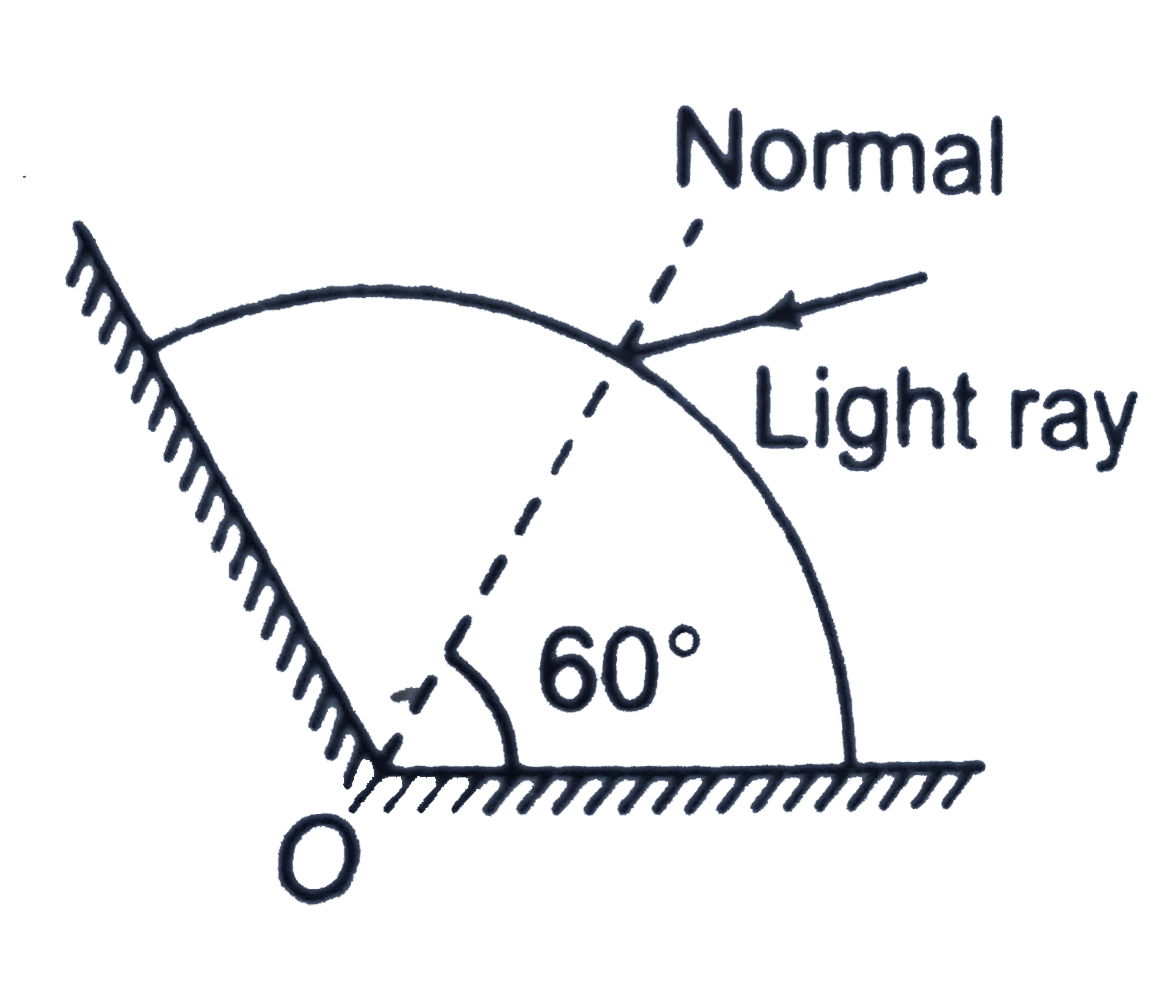
View SolutionConsider the situation as shown in figure. The point O is the centre. The light ray forms an angle of 60∘ with the horizontal and each mirror makes an angle 60∘ with the normal. The value of refractive index of that spherical portion so that light ray retraces its path is
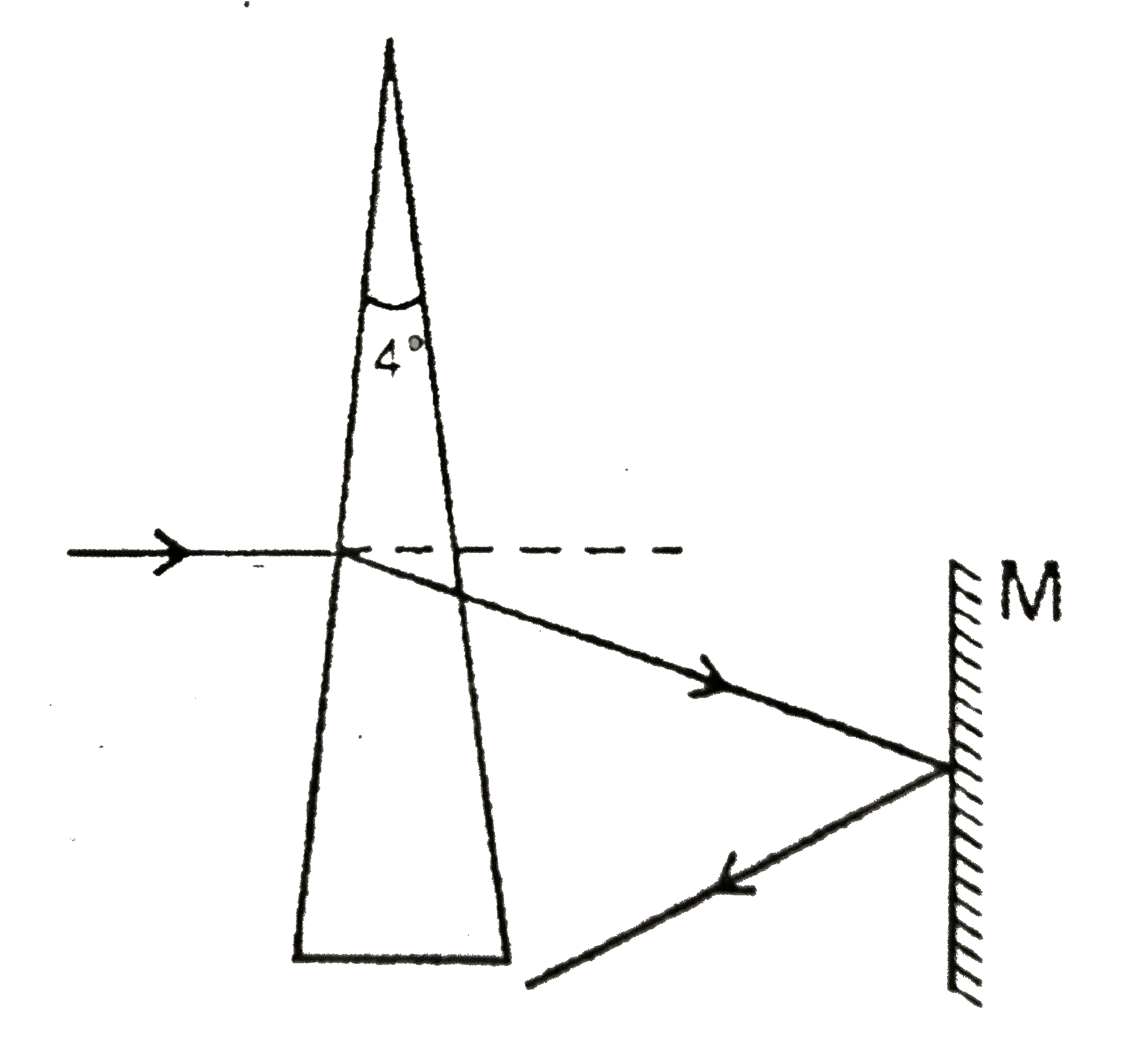
View SolutionA horizontal ray of light passes through a prism whose apex angle is 4∘ and then strikes a vertical mirror M as shown in Figure. For the ray to become horizontal after reflection, Find the angle by which the mirror must be rotated.
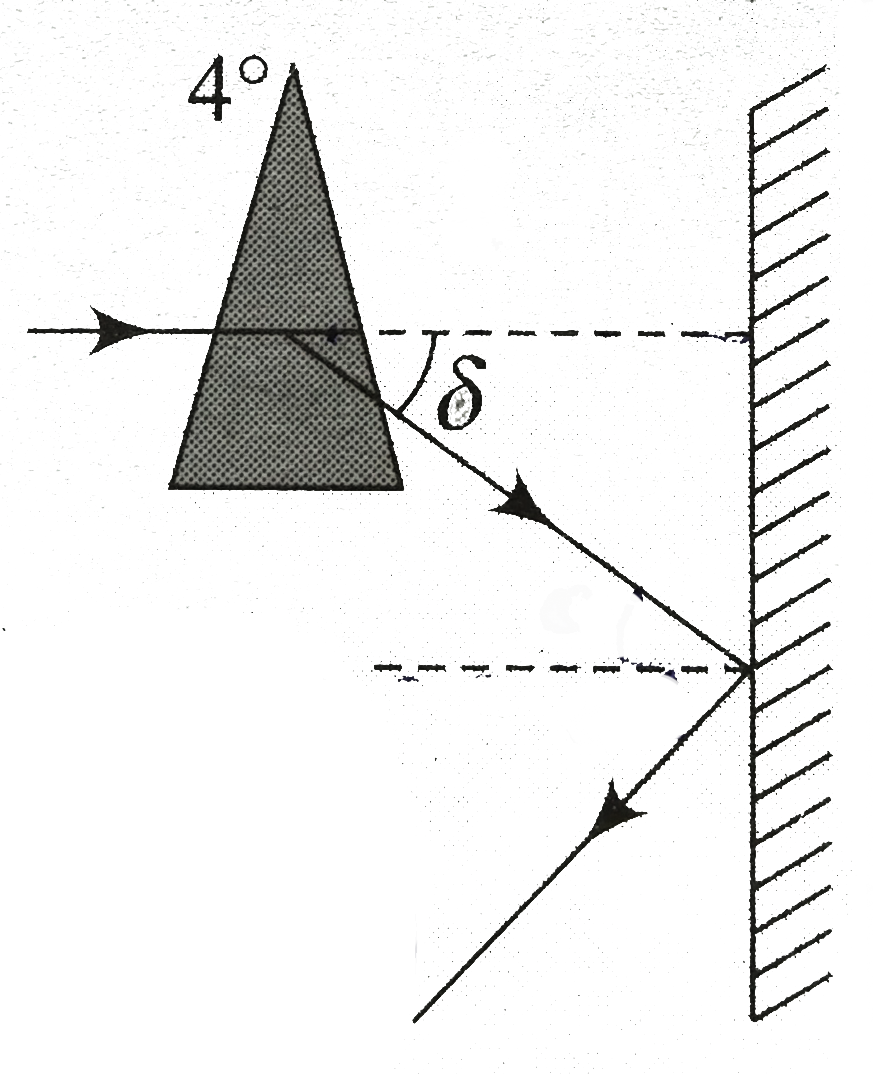
View SolutionA ray of light falls on a right angled prism ABC (AB=BC) and travels as shown in figure. What is the refractive index of material of the prism ?
View SolutionA point source S is placed midway between two converging mirrors having equal focal length f as shown in figure. Find the values of d for which only one image is formed.

View SolutionConsider the situation shown in figure. The two slite S1andS2
placed symmetrically around the centre line are illuminated by a monochromatic
light of wavelength lambda. The separation between the slits is d. The light transmitted
by the slits falls on a screen M1 placed at a distance D from the slits. The slit S3 is
at the centre line and the slit S4 is at a distance y form S3. Another screen M2 is
placed at a further distance D away from M1. Find the ration of the maximum to
minimum intensity observed on M2 if y is equal to (d<<D).
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

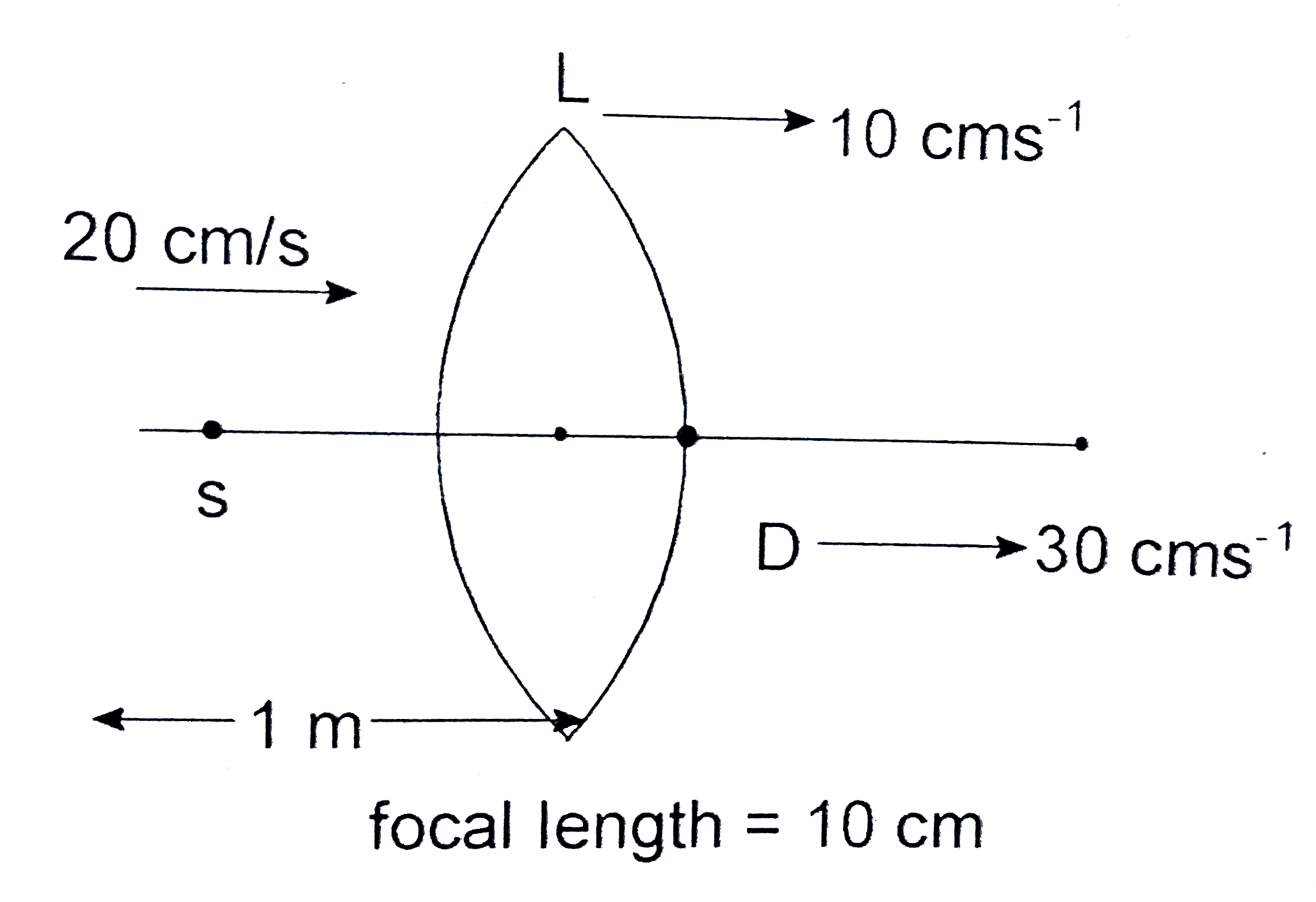
View SolutionThe figure shows the initial position of a point source of light s, a detector D and lens L. Now at t=0 all three starts moving toward right with different velocity as shown in figure. The times at which detector receives the maximum light.
View Solution
