If the sum of the roots of an equation is 2 and the sum of their cubes is 98, then find the equation.
The correct Answer is:x2−2x−15=0
To find the equation given the sum of the roots and the sum of their cubes, we can follow these steps:
Step 1: Define the roots.
Let the roots of the equation be α and β.
Step 2: Use the given information.
According to the problem, we have:
- The sum of the roots:
α+β=2
- The sum of the cubes of the roots:
α3+β3=98
Step 3: Use the identity for the sum of cubes.
We can use the identity for the sum of cubes:
α3+β3=(α+β)(α2−αβ+β2)
We can also express α2+β2 in terms of α+β and αβ:
α2+β2=(α+β)2−2αβ
Step 4: Substitute known values.
Substituting α+β=2 into the identity gives:
α3+β3=2(α2−αβ+β2)
Now substituting α2+β2:
α3+β3=2((α+β)2−3αβ)
Substituting α+β=2:
α3+β3=2(22−3αβ)=2(4−3αβ)=8−6αβ
Step 5: Set up the equation.
Now we know that:
8−6αβ=98
Rearranging gives:
−6αβ=98−8
−6αβ=90
Dividing both sides by -6:
αβ=−15
Step 6: Form the quadratic equation.
Now we have both the sum and product of the roots:
- α+β=2
- αβ=−15
The quadratic equation can be formed using the standard form:
x2−(α+β)x+αβ=0
Substituting the values:
x2−2x−15=0
Final Equation:
Thus, the required equation is:
x2−2x−15=0
---
Let the roots of the equation be α and β.
According to the problem, we have:
- The sum of the roots:
α+β=2
- The sum of the cubes of the roots:
α3+β3=98
We can use the identity for the sum of cubes:
α3+β3=(α+β)(α2−αβ+β2)
We can also express α2+β2 in terms of α+β and αβ:
α2+β2=(α+β)2−2αβ
Substituting α+β=2 into the identity gives:
α3+β3=2(α2−αβ+β2)
Now substituting α2+β2:
α3+β3=2((α+β)2−3αβ)
Substituting α+β=2:
α3+β3=2(22−3αβ)=2(4−3αβ)=8−6αβ
Now we know that:
8−6αβ=98
Rearranging gives:
−6αβ=98−8
−6αβ=90
Dividing both sides by -6:
αβ=−15
Now we have both the sum and product of the roots:
- α+β=2
- αβ=−15
x2−(α+β)x+αβ=0
Substituting the values:
x2−2x−15=0
Thus, the required equation is:
x2−2x−15=0
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.105videos
THEORY OF EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.118videos
THEORY OF EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.811videos
THEORY OF EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions294videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
The sum of an infinite G.P. is 57 and the sum of their cubes is 9457, find the G.P.
View SolutionThe sum of an infinite G.P. is 57 and the sum of their cubes is 9457, find the G.P.
View SolutionThe sum of three numbers in A.P. is 12 and the sum of their cubes is 288. Find the numbers.
View SolutionThe sum of infinite number of terms of a G.P. is 4 and the sum of their cubes is 192. Find the series.
View SolutionSum of the roots of the equation x2+7x+10=0
View SolutionIf the sum of two numbers is 5 and the sum of their cubes is 35, find the sum of their squares
View SolutionIf the sum of the roots of the equation x2+px+q=0 is 3 times their difference, then
View SolutionThe sum of two numbers is 7 and the sum of their cubes is 133. Find the sum of their squares
View SolutionConsider the graph of y = f(x) as shown in the following figure.
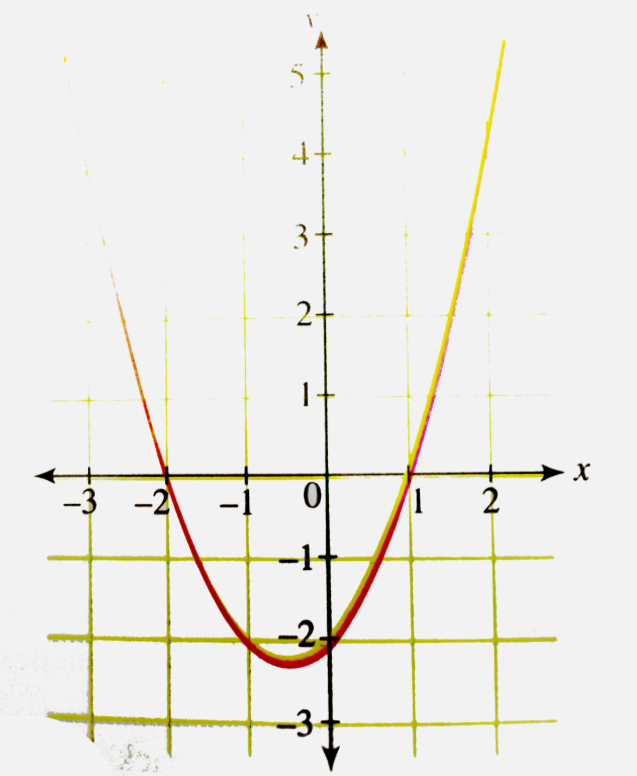
(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .View SolutionIf the sum of the roots of the equation ax2+bx+c=0 is equal to sum of the squares of their reciprocals, then bc2,ca2,ab2 are in
View Solution
