Question

Find the area of the smaller region bounded by the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
and the straight line $\frac{x}{a}+\frac{y}{b}=1.$

Explanation

Given ellips is Find the area between the ellpise `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
Given lines `(|x|)/(a)+(|y|)/(b)=1` formed a parallelogram whose diagonals are major axes of the given ellips.

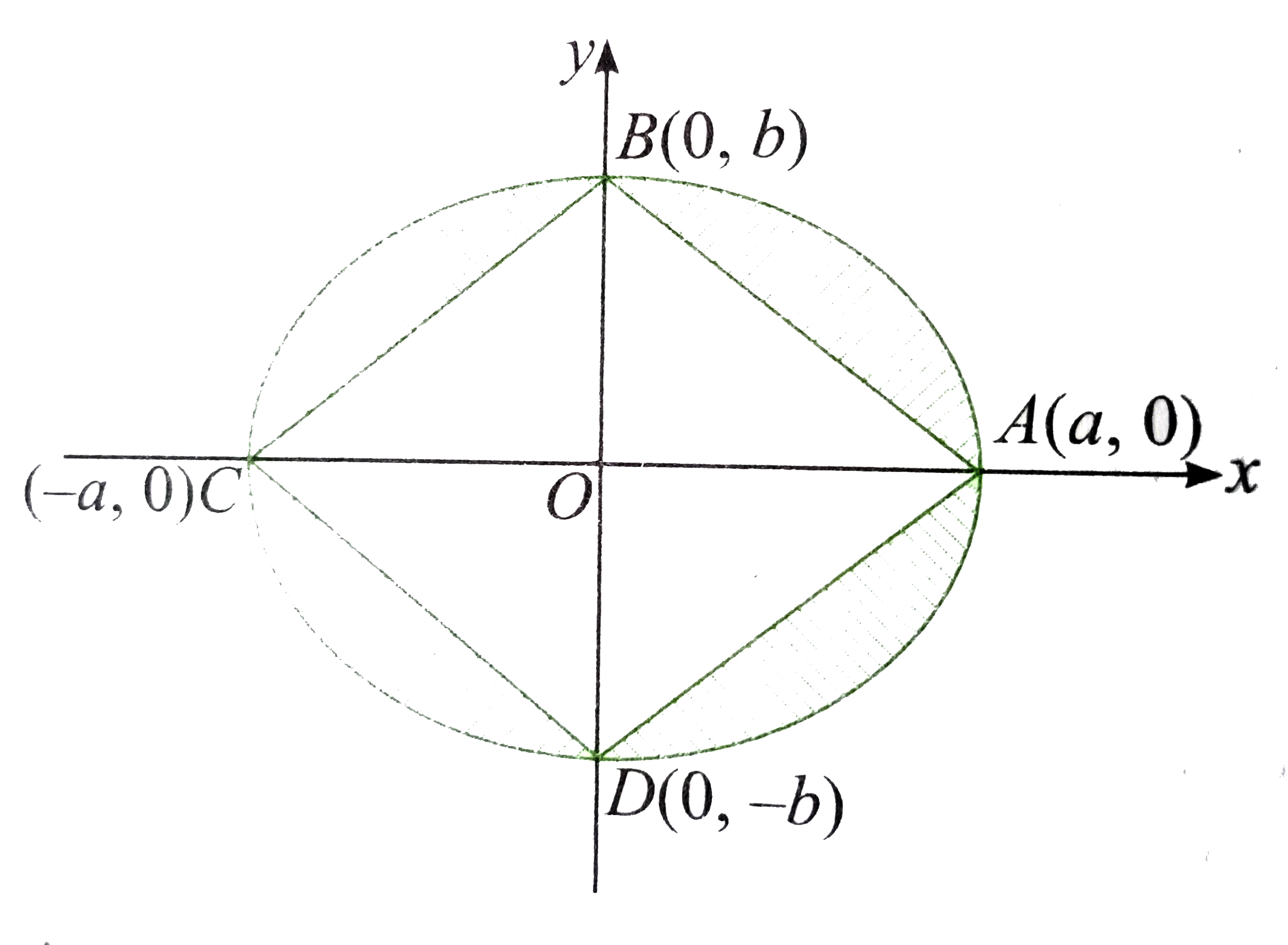
Required region shaded region in the figure.
`:.` Required area= Area of ellipse-Area of paralllogram
`=piab-4xx(1)/(2)ab=(pi-2)ab`