Question

Tangents PA and PB are drawn to the circle ${(x-4)}^2+{(y-5)}^2=4$ from the point P on the curve$y=\sin x$ , where A and B lie on the circle. Consider the function $y=f\left(x\right)$ represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?

Options

A. `2pi`
B. `3pi`
C. `pi`
D. not defined

Answer

3

Explanation

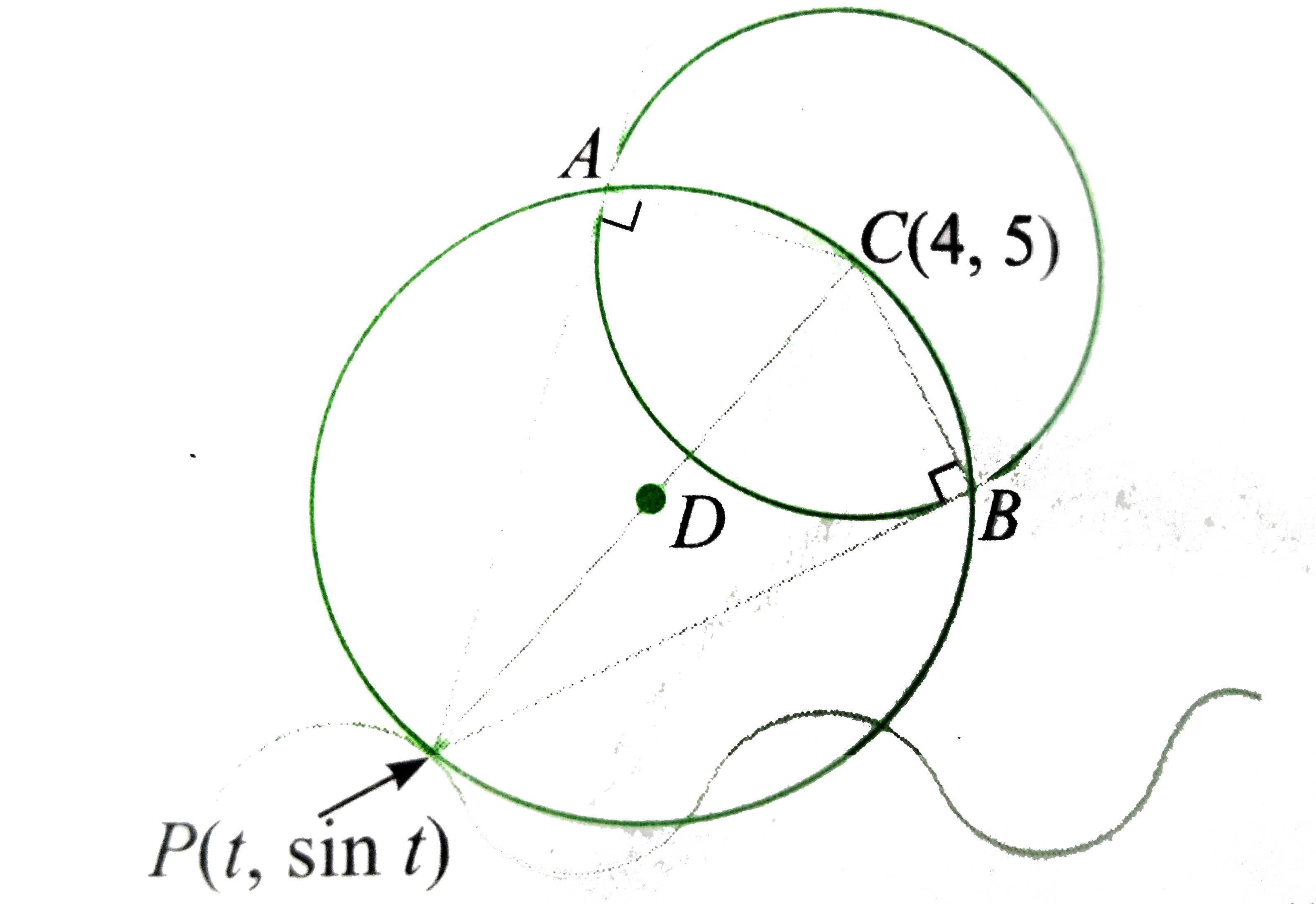
The center of the given circle is `C(4,5)` . Points P,A,C, and B are concyclic such that PC is the diameter of the circle. Hence, the center D(h,k) of the circumcircle of `Delta ABC` is the midpoint of PC.
Then, we have
`h=(t+4)/(2)` and `k =(sin t +5)/(2)`
Eliminating t, we have
`k=(sin (2h-4)+5)/(2)`
or `y=f(x)=(sin (2x-4)+5)/(2)`
`:. f^(-1)(x) = (sin^(-1)(2x-5)+4)/(2)`
Thus, the range of
`y=(sin (2x-4)+5)/(2)`
is `[2,3]` and the priod is `pi`.
Al,so `f(x)=4`, i.e.., `sin (2x-4)=3` which has no real solutions.
For `f(x) =1, sin (2x-4) = 3` which has no real solutions.
But range of `y= (sin ^(-1)(2x-5)+4)/(2) ` is `[-(pi)/(3) +2,(pi)/(4)+2]`