Find the equation of the circle whose radius is 3 and which touches internally the circle $x^{2} + y^{2} - 4 x - 6 y = - 12 = 0$ at the point $(- 1, - 1) .$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $5 x^{2} + 5 y^{2} - 8 x - 14 y - 32 = 0$

The given circle is
$x^{2} + y^{2} - 4 x - 6 y - 12 = 0$
whose center is $C_{1} (2, 3)$ and radius $r_{1}$ is $C_{1} A = 5$ .
If $C_{2} (h, k)$ is the centre of the circle of radius 3 which touches the circle (1) internally at $A (- 1, - 1)$ , then $C_{2} A = 3$ and $C_{1} C_{2} = C_{1} A - C_{2} A = 5 - 3 = 2$ .
Thus, $C_{2} (h, k)$ divides $C_{1}$ A in the ratio $2 : 3$ internally. Therefore,
$h = \frac{2 (- 1) + 3 \times 2}{2 + 3} = \frac{4}{5}$
and $k = \frac{2 (- 1) + 3 \times 3}{2 + 3} = \frac{7}{5}$
Hence, the equaiton of the required circle is ${(x - 4 / 5)}^{2} + {(y - 7 / 5)}^{2} = 3^{2}, i . e ., 5 x^{2} + 5 y^{2} - 8 x - 14 y - 32 = 0$ .

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

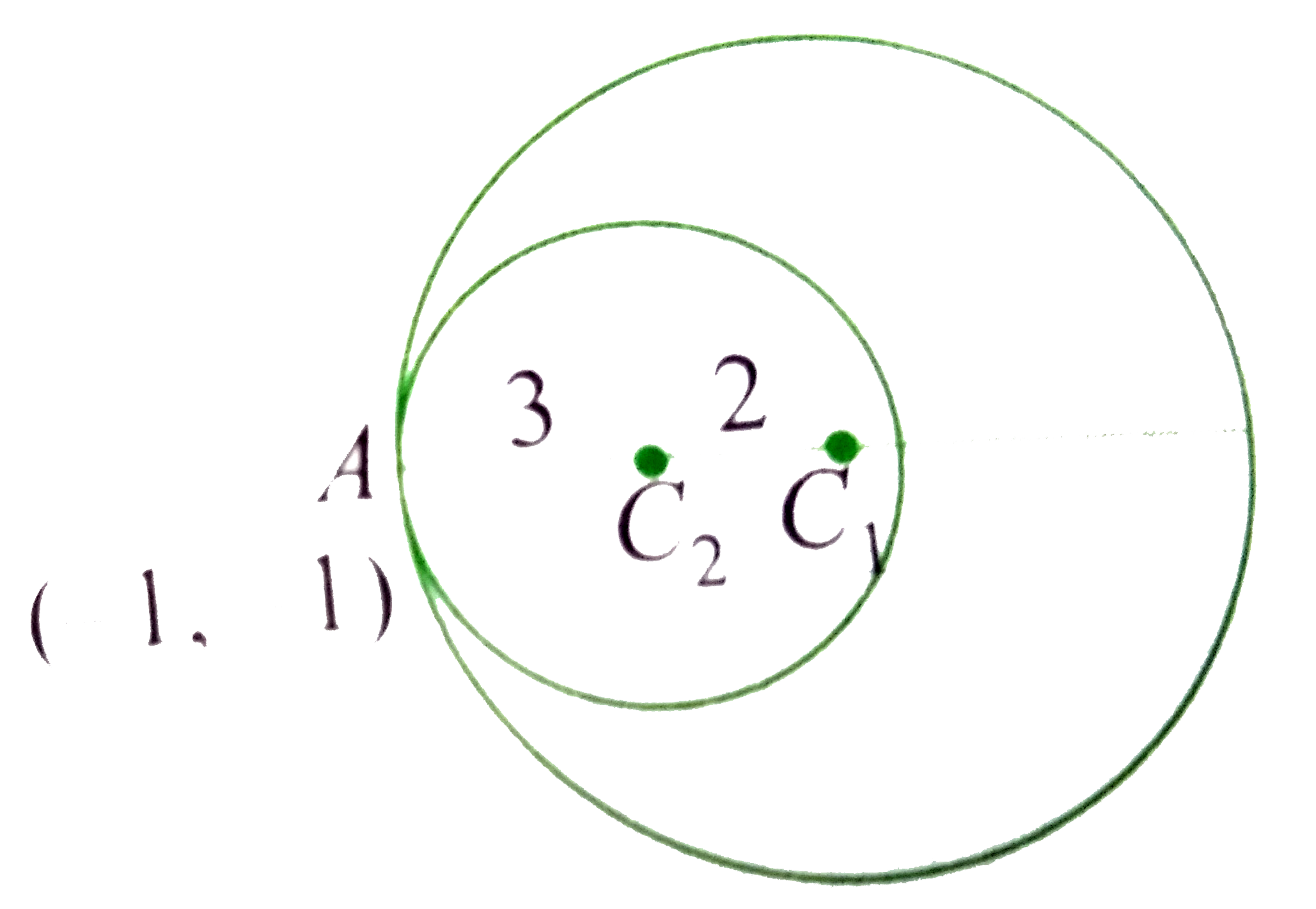
Topper's Solved these Questions

Similar Questions

Knowledge Check

The equation of the circle whose center is (3,-2) and which touches the line $3 x - 4 y + 13 = 0$ is
AA. $x^{2} + y^{2} + 6 x - 4 y - 23 = 0$
BB. $x^{2} + y^{2} - 6 x - 4 y - 23 = 0$
CC. $x^{2} + y^{2} - 6 x + 4 y - 23 = 0$
DD. $x^{2} + y^{2} + 6 x + 4 y + 23 = 0$

CENGAGE ENGLISH-CIRCLE -CONCEPT APPLICATION EXERCISE 4.13

Home
Ask Doubt
Profile