If the perimeter of the triangle formed by feet of altitudes of the triangle ABC is equal to four times the circumradius of ΔABC, then identify the type of ΔABC
The correct Answer is:Triangle is not possible
To solve the problem, we need to analyze the given information about triangle ABC and the triangle formed by the feet of the altitudes of triangle ABC.
1. Understanding the Problem: We are given that the perimeter of the triangle formed by the feet of the altitudes of triangle ABC (let's call it triangle DEF) is equal to 4 times the circumradius (R) of triangle ABC. We need to identify the type of triangle ABC.
2. Setting Up the Equation: The perimeter of triangle DEF is given by:
DE+EF+FD=4R
3. Using the Lengths of the Feet of Altitudes: The lengths of the segments formed by the feet of the altitudes can be expressed in terms of the sides of triangle ABC:
- DE=bcosC
- EF=ccosA
- FD=acosB
Thus, we can rewrite the perimeter equation as:
acosB+bcosC+ccosA=4R
4. Applying the Sine Rule: According to the sine rule, we have:
a=2RsinA,b=2RsinB,c=2RsinC
5. Substituting into the Perimeter Equation: Substitute the expressions for a, b, and c into the perimeter equation:
(2RsinAcosB)+(2RsinBcosC)+(2RsinCcosA)=4R
6. Simplifying the Equation: Dividing through by 2R (assuming R≠0):
sinAcosB+sinBcosC+sinCcosA=2
7. Using the Double Angle Identity: Recall that sinAcosB=12sin(2A). Thus, we can express the left-hand side as:
12sin(2A)+12sin(2B)+12sin(2C)=2
Multiplying through by 2 gives:
sin(2A)+sin(2B)+sin(2C)=4
8. Analyzing the Sine Function: The maximum value of sin(x) is 1. Therefore, the maximum value of sin(2A)+sin(2B)+sin(2C) can be at most 3. The equation sin(2A)+sin(2B)+sin(2C)=4 cannot hold true because it exceeds the maximum possible sum of 3.
9. Conclusion: Since the condition leads to a contradiction, the only way this can happen is if triangle ABC is a right-angled triangle. In a right triangle, one angle is 90∘ (or π2), which makes the sine of that angle equal to 1, thus allowing for the possibility of the equation to balance out.
Final Answer:
Triangle ABC is a right-angled triangle.
DE+EF+FD=4R
- DE=bcosC
- EF=ccosA
- FD=acosB
acosB+bcosC+ccosA=4R
a=2RsinA,b=2RsinB,c=2RsinC
(2RsinAcosB)+(2RsinBcosC)+(2RsinCcosA)=4R
sinAcosB+sinBcosC+sinCcosA=2
12sin(2A)+12sin(2B)+12sin(2C)=2
Multiplying through by 2 gives:
sin(2A)+sin(2B)+sin(2C)=4
Triangle ABC is a right-angled triangle.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.10
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.11
4 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.8
7 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
Knowledge Check
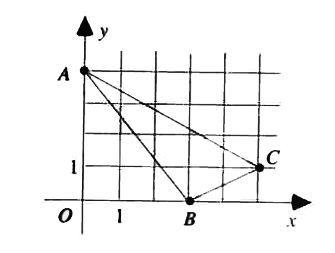
In the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2In the figure, what is the area of ΔABC?
 A6B7C8DIt cannot be determined from the information given
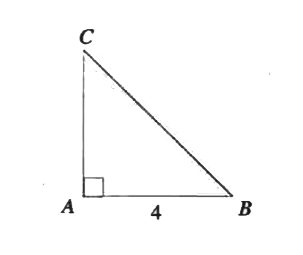
A6B7C8DIt cannot be determined from the information givenWhat is the perimenter of Triangle ABC in the figure?
 A5+√5+√34B10+√34C5+√5+√28D2√5+√34
A5+√5+√34B10+√34C5+√5+√28D2√5+√34
H is orthocenter of the triangle ABC, then AH is equal to :
View SolutionIf the radius of the circumcircle of the isosceles triangle ABC is equal to AB(=AC), then the angle A is equal to-
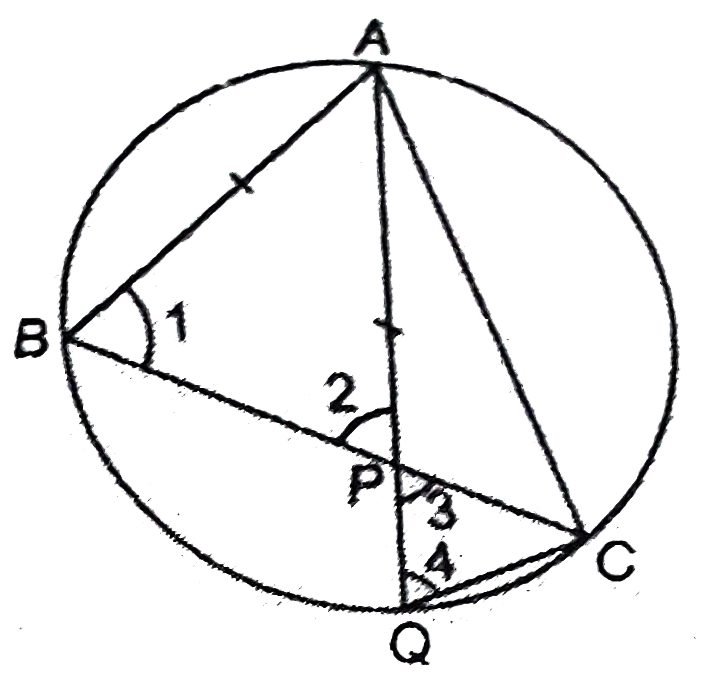
View SolutionIn given figure , ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
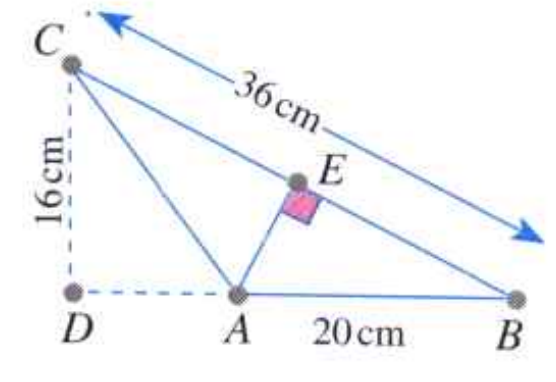
View SolutionIn the given triangle ABC, find AE.
View SolutionIn triangle ABC, R(b+c)=a√bc, where R is the circumradius of the triangle. Then the triangle is
View Solution
