Two whole numbers are randomly selected and multiplied. Consider two events E1andE2 defined as E1 : Their product is divisible by 5 and E2 Unit's place in their product is 5 Which of the following statement(s) is/are correct?
E1 is twice as likely to occur as E2
E1andE2 are disjoint
P(E2/E1)=1/4
P(E1/E2)=1
The correct Answer is:C, D
To solve the problem, we need to analyze the two events E1 and E2:
1. Event E1: The product of the two selected numbers is divisible by 5.
2. Event E2: The unit's place of the product is 5.
Step 1: Calculate the probability of E1
To find the probability of E1, we need to determine the conditions under which the product of two numbers is divisible by 5.
- A product is divisible by 5 if at least one of the numbers is divisible by 5.
- The possible unit digits of whole numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
- Among these, the digits that contribute to divisibility by 5 are 0 and 5.
The probability that a randomly selected whole number does not end with 0 or 5 (i.e., ends with 1, 2, 3, 4, 6, 7, 8, or 9) is 810=45.
Thus, the probability that both selected numbers do not end with 0 or 5 is:
P(both not ending with 0 or 5)=(45)×(45)=1625
Therefore, the probability that at least one of them ends with 0 or 5 (which means the product is divisible by 5) is:
P(E1)=1−P(both not ending with 0 or 5)=1−1625=925
Step 2: Calculate the probability of E2
Next, we calculate the probability of E2. The unit's place of the product of two numbers will be 5 if:
- One number ends with 5 and the other ends with an odd digit (1, 3, 5, 7, 9).
The probability that a randomly selected number ends with 5 is 110, and the probability that it ends with an odd digit (1, 3, 5, 7, 9) is 510=12.
Thus, the probability that one number ends with 5 and the other ends with an odd digit can be calculated as:
P(E2)=P(first number ends with 5)×P(second number ends with odd digit)+P(first number ends with odd digit)×P(second number ends with 5)
This gives us:
P(E2)=(110×12)+(12×110)=120+120=220=110
Step 3: Calculate the conditional probability P(E2|E1)
Now we need to find the conditional probability P(E2|E1):
P(E2|E1)=P(E2∩E1)P(E1)
Since E2 (unit's place is 5) implies E1 (product is divisible by 5), we can say:
P(E2∩E1)=P(E2)
Thus:
P(E2|E1)=P(E2)P(E1)=110925=110×259=2590=518
Conclusion
Based on the calculations:
- P(E1)=925
- P(E2)=110
- P(E2|E1)=518
2. Event E2: The unit's place of the product is 5.
- The possible unit digits of whole numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
- Among these, the digits that contribute to divisibility by 5 are 0 and 5.
P(both not ending with 0 or 5)=(45)×(45)=1625
P(E1)=1−P(both not ending with 0 or 5)=1−1625=925
- One number ends with 5 and the other ends with an odd digit (1, 3, 5, 7, 9).
P(E2)=P(first number ends with 5)×P(second number ends with odd digit)+P(first number ends with odd digit)×P(second number ends with 5)
This gives us:
P(E2)=(110×12)+(12×110)=120+120=220=110
P(E2|E1)=P(E2∩E1)P(E1)
P(E2∩E1)=P(E2)
P(E2|E1)=P(E2)P(E1)=110925=110×259=2590=518
- P(E1)=925
- P(E2)=110
- P(E2|E1)=518
Topper's Solved these Questions
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - LINKED COMPREHENSION TYPE
43 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MATRIX MATCH TYPE
10 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - EXERCISE
68 Videos
- PROBABILITY I BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - JEE Advanced
7 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
Similar Questions
Two numbers are randomly selected and multiplied. Consider two events E1andE2 defined as E1 : Their product is divisible by 5 and E2 Unit's place in their product is 5 Which of the following statement(s) is/are correct? (a)E1 is twice as likely to occur as E2. (b) E1 and E2 are disjoint. (c) P(E1/E2)=1/4 (d) P(E1/E2)=1
View SolutionFor the equation e−xx+1 which of the following statement(s) is/are correct ?
View Solution
Knowledge Check
The E2 product of the following reaction will be ?
 A
A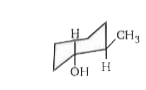 B
B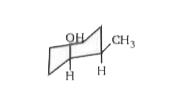 C
C D
D
Consider the following E1/SN1 reaction
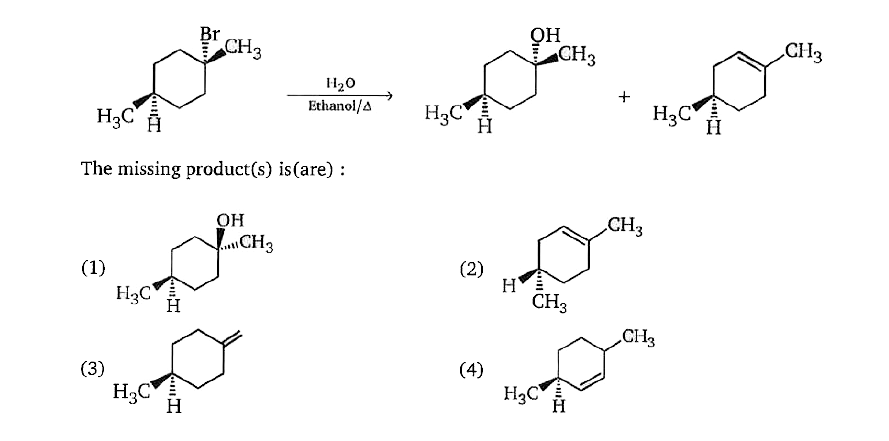 A1,2 and 3B3 and 4C2 and 3D1,2,3 and 4
A1,2 and 3B3 and 4C2 and 3D1,2,3 and 4
Two whole numbers are randomly chosen and multiplied, then the chance that their product is divisible by 5 is
View SolutionLet limx→∞(2x+ax+ex)1/x=L which of the following statement (s) is (are) correct ?
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
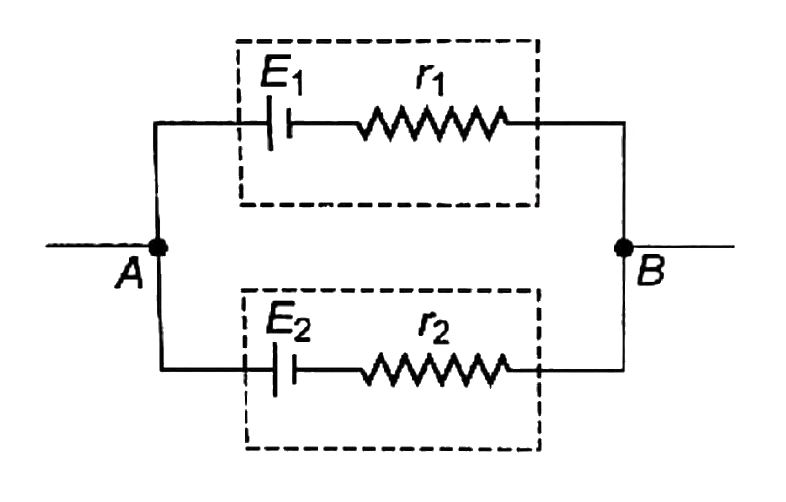
View SolutionThe activation energies of two reactions are Ea1 and Ea2 with Ea1>Ea2. If the temperature of the reacting systems is increased from T to T', which of the following is correct?
View SolutionThe activation energies of two reactions are Ea1 and Ea2 with Ea1>Ea2. If the temperature of the reacting systems is increased from T to T', which of the following is correct?
View SolutionLet two fair six-faced dice A and B be thrown simultaneously. If E1 is the event that die A shows up four, E2 is the event that die B shows up two and E3 is the event that the sum of numbers on both dice is odd, then which of the following statements is NOT true ? (1) E1 and E2 are independent. (2) E2 and E3 are independent. (3) E1 and E3 are independent. (4) E1 , E2 and E3 are independent.
View Solution
