If a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
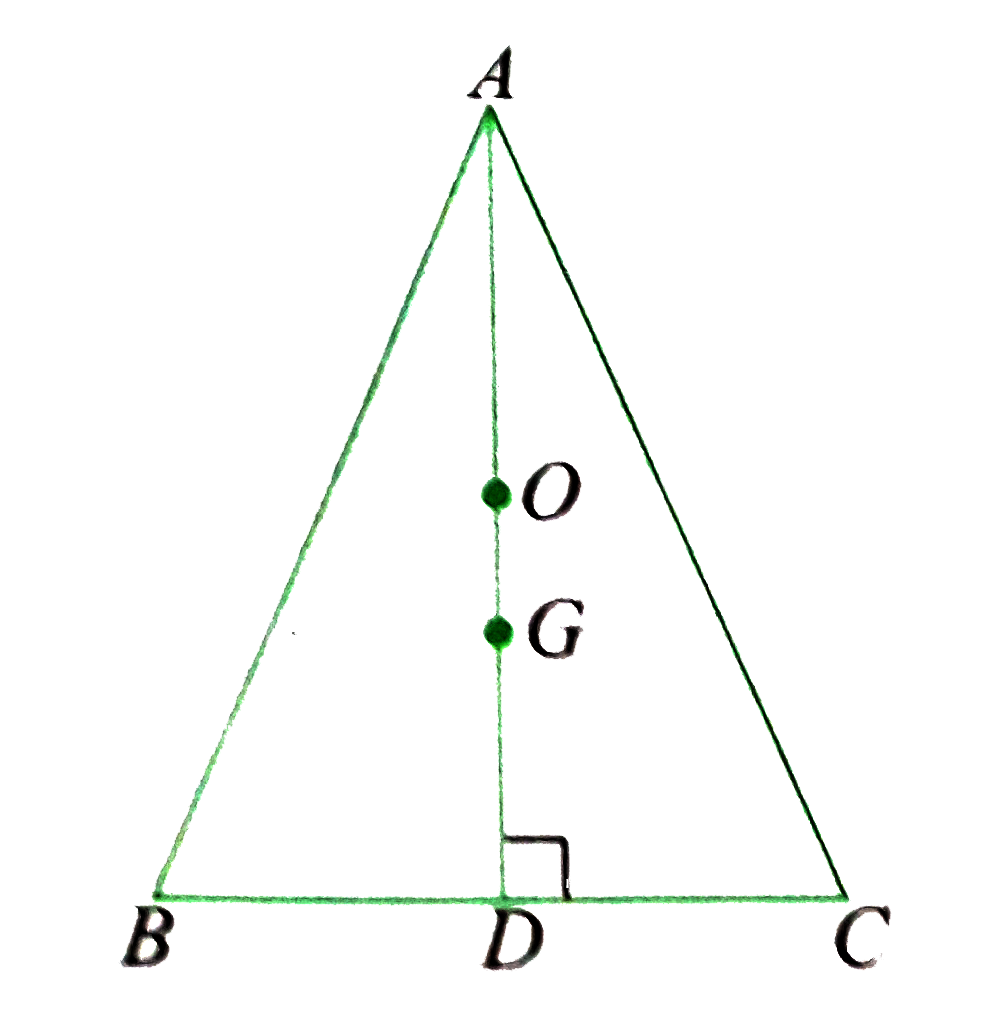
We have vertex A(0,0) circumcentre O(3,4) and centroid G(6,8). Point O lies on the perpendicular bisector (OD) of side BC and point G lies on the median AD.
Now, A O and G are collinear. So median AD and perpendicular bisector (OD) of BC coincide. Thus, AD is the perpendicular bisector of BC. Therefore, triangle ABC is isosceles.
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGE ENGLISHChapter:COORDINATE SYSYEM Exercise:Illustration1.34
Explore 1 Video
- COORDINATE SYSYEM Book:CENGAGE ENGLISHChapter:COORDINATE SYSYEM Exercise:Illustration1.35
Explore 1 Video
- COORDINATE SYSYEM Book:CENGAGE ENGLISHChapter:COORDINATE SYSYEM Exercise:Illustration1.32
Explore 1 Video
- COORDINATE SYSTEMBook:CENGAGE ENGLISHChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGE ENGLISHChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
A triangle whose all sides are equal is called
View SolutionCan an acute-angled triangled be a. and equilateral, b. an isosceles, and c. a scalene triangle ?
View SolutionDetermine the measure of each of the equal angles of a right-angled isosceles triangle.
View SolutionIf the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is a right-angle triangle.
View SolutionA triangle whose two sides are equal is called (a) an acute triangle (b) a scalene triangle (c) an isosceles triangle (d) an equilateral triangle
View SolutionIf the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is right-angled triangle.
View SolutionIn figure ABC is an isosceles triangle , right angled at C . Therefore
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is (a) an isosceles triangle (b) an obtuse triangle (c) an equilateral triangle (d) a right triangle
View SolutionIdentify the following triangles as equilateral, isosceles, scalene, acute-angled, right-angled, and obtuse-angled triangles.
View SolutionA triangle whose two sides are equal is known as
View Solution

