Solve sin−1x>tan−1x
Video Solution
Text Solution
The correct Answer is:x∈(0,1)
We have sin−1x<tan−1x
Given inequality is meaningful if x∈[−1,1].
Now, let's draw the graph of y=sin−1xandy=tan−1x.
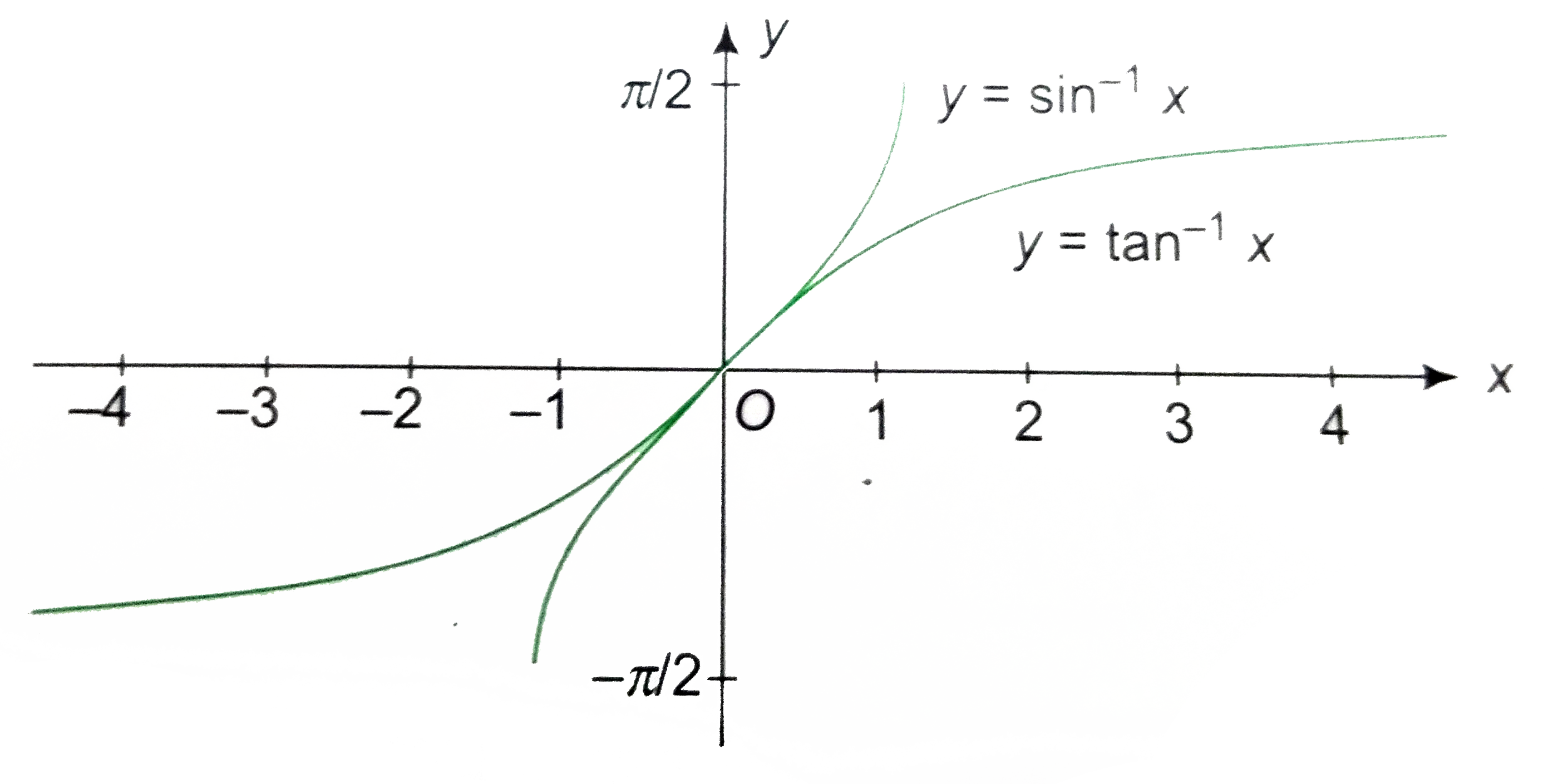
From the graph, we can see that sin−1x>tan−1x for x∈(0,1]
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.2
6 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.3
12 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Illustration
85 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE
3 Videos
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
Similar Questions
Solve tan−1x>cot−1x
View SolutionSolve sin−1x>−1
View SolutionStatement I sin−1(1√e)>tan−1(1√π)
Statement II sin−1x>tan−1y for x>y,∀x,y∈(0,1)
View SolutionSolve sec−1x>cosec−1x
View SolutionSolve : tan−1x+tan−1(2x1−x2)=π3
View SolutionSolve : sin−1x+sin−12x=π3
View SolutionSolve tan−1x+sin−1x=tan−12x
View SolutionSolve tan−1x+cot−1(−|x|)=2tan−16x
View SolutionSolve: ∫1−1xtan−1xdx
View SolutionSolve: tan−1(2+x)+tan−1(2−x)=tan−123
View Solution
