Question

Plot $y=\sin xandy=\sin 2x\stackrel{.}{}$

Explanation

We have `y=sin2x.`
Since the period of `y=sin2x" is "(2pi)/(2)=pi`, the graph completes its one cycle in the interval of length `pi`.
In any interval of length `pi`, sin 2x takes all its values, which are [-1,1].
So graph of `y=sin2x" for "x in[0,pi]` is as follows.

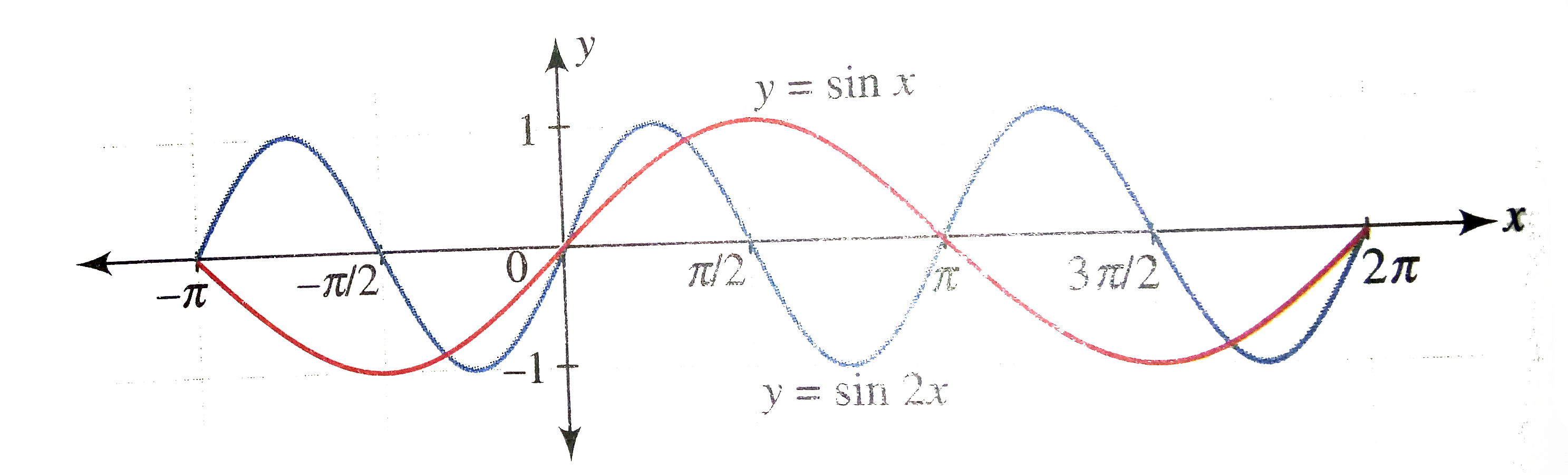
Thus, the graph of `y=sinx` is compressed by 2 units horizontally.
In `[0,2pi],y=sin2x` completes its two cycles.