The mean deviation about the median of the following distribution is
Marks obtained1011121415Number of students23834
The correct Answer is:B
To find the mean deviation about the median for the given distribution, we will follow these steps:
Step 1: Create the Frequency Table
We have the following data:
| Marks Obtained (xi) | Number of Students (fi) |
|----------------------|-------------------------|
| 10 | 2 |
| 11 | 3 |
| 12 | 8 |
| 14 | 3 |
| 15 | 4 |
Step 2: Calculate Cumulative Frequency
We will calculate the cumulative frequency (cf):
| Marks Obtained (xi) | Number of Students (fi) | Cumulative Frequency (cf) |
|----------------------|-------------------------|----------------------------|
| 10 | 2 | 2 |
| 11 | 3 | 5 |
| 12 | 8 | 13 |
| 14 | 3 | 16 |
| 15 | 4 | 20 |
Step 3: Find the Total Frequency
The total frequency N is the last cumulative frequency value, which is 20.
Step 4: Calculate the Median
To find the median, we calculate N2=202=10. We find the cumulative frequency that is just greater than or equal to 10. This corresponds to the value 12.
Thus, the median M is 12.
Step 5: Calculate Deviations
Now we will calculate the deviations di=xi−M:
| Marks Obtained (xi) | Number of Students (fi) | Deviation (di = xi - M) |
|----------------------|-------------------------|--------------------------|
| 10 | 2 | 10 - 12 = -2 |
| 11 | 3 | 11 - 12 = -1 |
| 12 | 8 | 12 - 12 = 0 |
| 14 | 3 | 14 - 12 = 2 |
| 15 | 4 | 15 - 12 = 3 |
Step 6: Calculate fi⋅di
Now we will calculate fi⋅di:
| Marks Obtained (xi) | Number of Students (fi) | Deviation (di) | fi⋅di |
|----------------------|-------------------------|-----------------|----------------------|
| 10 | 2 | -2 | 2 * -2 = -4 |
| 11 | 3 | -1 | 3 * -1 = -3 |
| 12 | 8 | 0 | 8 * 0 = 0 |
| 14 | 3 | 2 | 3 * 2 = 6 |
| 15 | 4 | 3 | 4 * 3 = 12 |
Step 7: Sum of fi⋅di
Now we sum up the values of fi⋅di:
∑fi⋅di=−4−3+0+6+12=11
Step 8: Calculate Mean Deviation
Finally, we calculate the mean deviation about the median using the formula:
Mean Deviation=∑fi⋅diN=1120=0.55
Final Answer
The mean deviation about the median is 0.55.
---
We have the following data:
|----------------------|-------------------------|
| 10 | 2 |
| 11 | 3 |
| 12 | 8 |
| 14 | 3 |
| 15 | 4 |
We will calculate the cumulative frequency (cf):
|----------------------|-------------------------|----------------------------|
| 10 | 2 | 2 |
| 11 | 3 | 5 |
| 12 | 8 | 13 |
| 14 | 3 | 16 |
| 15 | 4 | 20 |
The total frequency N is the last cumulative frequency value, which is 20.
To find the median, we calculate N2=202=10. We find the cumulative frequency that is just greater than or equal to 10. This corresponds to the value 12.
Now we will calculate the deviations di=xi−M:
|----------------------|-------------------------|--------------------------|
| 10 | 2 | 10 - 12 = -2 |
| 11 | 3 | 11 - 12 = -1 |
| 12 | 8 | 12 - 12 = 0 |
| 14 | 3 | 14 - 12 = 2 |
| 15 | 4 | 15 - 12 = 3 |
Now we will calculate fi⋅di:
|----------------------|-------------------------|-----------------|----------------------|
| 10 | 2 | -2 | 2 * -2 = -4 |
| 11 | 3 | -1 | 3 * -1 = -3 |
| 12 | 8 | 0 | 8 * 0 = 0 |
| 14 | 3 | 2 | 3 * 2 = 6 |
| 15 | 4 | 3 | 4 * 3 = 12 |
Now we sum up the values of fi⋅di:
Finally, we calculate the mean deviation about the median using the formula:
The mean deviation about the median is 0.55.
Topper's Solved these Questions
- STATISTICSBOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Exercise 11.1
5 Videos
- STATISTICSBOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Exercise 11.2
6 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type
6 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
Similar Questions
Find the mean deviation about the median for the following frequency distribution.

View SolutionFind the mean deviation about the median for the following continuous distribution.

View SolutionFind the mean for the following data.
Marks obtained10−2020−3030−4040−5050−6060−70Number of students8612527
View SolutionFind the median for the following frequency distribution :
Marks obtained(xi)293234274237Number of students(fi)25101284
View SolutionFind the mean deviation about median for the following continuous frequency distribution data
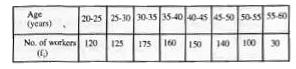
View SolutionFind the mean deviation about the median for the following data:4,6,9,3,10,13,2
View SolutionFind the mean deviation about the mean for the following data: Marks obtained , 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80 Number of students, 2, 3, 8, 14, 8, 3, 2
View Solutionmean deviation about median for the following data 2,5,7,2,4,6,10,12,5
View SolutionFind the mean deviation about the median for the following data:
11, 3, 8, 7, 5, 14, 10, 2, 9
View SolutionFind the mean deviation about the mean for the following data: Marks obtained 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Number of students 2 3 8 14 8 3 2
View Solution
