Two men start with velocity at the same time from the junction of two roads inclined at to each other. If they travel by different roads, find the rate at which they are being separated.
To solve the problem of finding the rate at which two men P and Q are being separated as they travel along two roads inclined at 45 degrees to each other, we can follow these steps:
Step 1: Understanding the Problem
We have two men starting from the same point and moving away from each other along two roads that form a 45-degree angle. Both men have the same initial velocity, denoted as u.
Step 2: Representing Their Velocities
Let’s denote the velocity of man P as v1 and the velocity of man Q as v2. Since both men are moving at the same speed u, we have:
- |v1|=u
- |v2|=u
Step 3: Components of the Velocities
Since the roads are inclined at 45 degrees, we can resolve the velocities into components. The horizontal component of the velocity for man Q can be expressed as:
v1=ucos(45∘)=u⋅1√2=u√2
And the vertical component for man P remains:
v2=usin(45∘)=u⋅1√2=u√2
Step 4: Finding the Rate of Separation
The rate at which they are separating can be found using the formula for the relative velocity between the two men. The separation velocity vs can be calculated as:
vs=|v2|−|v1|
Substituting the values we found:
vs=u−u√2
Factoring out u:
vs=u(1−1√2)
Step 5: Simplifying the Expression
To simplify 1−1√2:
1−1√2=√2−1√2
Thus, the rate of separation becomes:
vs=u⋅√2−1√2
Final Answer
The rate at which the two men are being separated is:
u(√2−1)√2
We have two men starting from the same point and moving away from each other along two roads that form a 45-degree angle. Both men have the same initial velocity, denoted as u.
Let’s denote the velocity of man P as v1 and the velocity of man Q as v2. Since both men are moving at the same speed u, we have:
- |v1|=u
- |v2|=u
Since the roads are inclined at 45 degrees, we can resolve the velocities into components. The horizontal component of the velocity for man Q can be expressed as:
v1=ucos(45∘)=u⋅1√2=u√2
And the vertical component for man P remains:
v2=usin(45∘)=u⋅1√2=u√2
The rate at which they are separating can be found using the formula for the relative velocity between the two men. The separation velocity vs can be calculated as:
vs=|v2|−|v1|
Substituting the values we found:
vs=u−u√2
Factoring out u:
vs=u(1−1√2)
To simplify 1−1√2:
1−1√2=√2−1√2
Thus, the rate of separation becomes:
vs=u⋅√2−1√2
The rate at which the two men are being separated is:
u(√2−1)√2
Similar Questions
Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45∘ to each other.If they travel by different roads,find the rate at which they are being separated.
View SolutionTwo cyclists start from the junction of two perpendicular roads, there velocities being 3um/m∈ and 4um/m∈ , respectively. Find the rate at which the two cyclists separate.
View SolutionTwo cyclists start from the junction of two perpendicular roads, there velocities being 3um/m∈ and 4um/m∈ , respectively. Find the rate at which the two cyclists separate.
View SolutionThe distance between two particles is decreasing at the rate of 6 m/sec,when they travel in opposite direction to each other. If these particles travel with same speeds and in the same direction, then the separation increase at the rate of 4 m/sec. The particles have speed as
View SolutionPlaces A and B are 100 km apart on a highway. One car starts from A and another from b at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars
View SolutionPlaces A and B are 100 km apart on a highway. One car starts from A and another from b at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars
View SolutionTwo ships leave port at the same time. One goes 24 km per hour in the direction N 450E and other travels 32 km per hour in the direction S750E. Find the distance between the ships at the end of 3 hours.
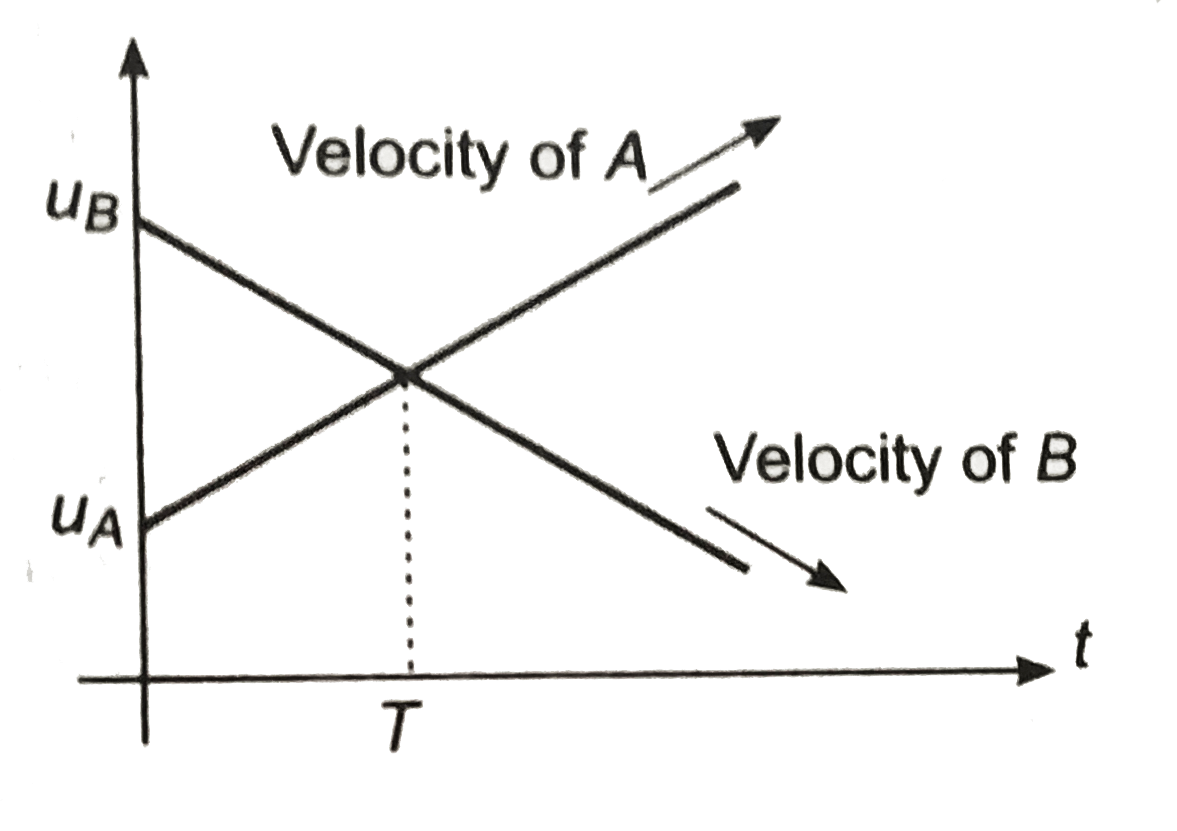
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
5. If the value of T is 4 s, then the time after which A will meet B is
View SolutionTwo particles P1 and P2 are performing SHM along the same line about the same mean position , initial they are at their extreme position. If the time period of each particle is 12 sec and the difference of their amplitude is 12cm then find the minimum time after which the separation between the particle becomes 6cm.
View SolutionThrough a rectangular field of sides 90 m × 60 m , two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the field. If the width of the roads is 3 m, find the total area covered by the two roads.
View Solution
