T1 is an isosceles triangle in circle C. Let T2 be another Ãsosceles triangle inscribed in C whose base is one of the equal sides of T1 and which overlaps the interior of T1. Similarly, create isosceles triangle T3 from T2;T4andT5, and so on. Prove that the triangle Tn, approaches an equilateral triangle as n→∞,
To prove that the triangle Tn approaches an equilateral triangle as n→∞, we will analyze the angles of the isosceles triangles T1,T2,T3,… inscribed in the circle.
1. Define Triangle T1:
Let T1 be an isosceles triangle inscribed in circle C with vertices A,B,C. Assume AB=AC and let the angle at vertex A be θ. Thus, the angles at vertices B and C are equal, and can be denoted as α.
Angle A=θ,Angle B=Angle C=α
Using the triangle angle sum property:
θ+2α=180∘⟹α=180∘−θ2
2. Define Triangle T2:
Triangle T2 is also an isosceles triangle inscribed in circle C with its base being one of the equal sides of T1 (say AB). Let the vertex opposite the base AB be C′. The angle at vertex C′ will also be θ.
By the same reasoning as before, the angles at A and B in triangle T2 will also be equal. Let these angles be β.
Angle C′=θ,Angle A=Angle B=β
Using the triangle angle sum property:
θ+2β=180∘⟹β=180∘−θ2
3. Relate Angles of Subsequent Triangles:
Continuing this process, for triangle T3, the angle at the vertex opposite the base will again be θ, and the angles at the other two vertices will be γ.
Angle C′′=θ,Angle A′=Angle B′=γ
Using the triangle angle sum property:
θ+2γ=180∘⟹γ=180∘−θ2
4. Establish a Pattern:
We can see a pattern forming:
- For Tn, the angle at the vertex opposite the base remains θ.
- The angles at the other two vertices are given by:
Angle An=Angle Bn=180∘−θ2
As n increases, the angles α,β,γ,… keep halving the remaining angle 180∘−θ.
5. Limit as n→∞:
As n approaches infinity, the angle θ approaches 60∘ (since the angles should sum to 180∘ and become equal). Thus, we can conclude that:
limn→∞θn=60∘
Therefore, the angles of triangle Tn approach:
Angle An=Angle Bn=Angle Cn=60∘
Hence, triangle Tn approaches an equilateral triangle.
Conclusion
Thus, we have shown that as n→∞, triangle Tn approaches an equilateral triangle.
Let T1 be an isosceles triangle inscribed in circle C with vertices A,B,C. Assume AB=AC and let the angle at vertex A be θ. Thus, the angles at vertices B and C are equal, and can be denoted as α.
θ+2α=180∘⟹α=180∘−θ2
Triangle T2 is also an isosceles triangle inscribed in circle C with its base being one of the equal sides of T1 (say AB). Let the vertex opposite the base AB be C′. The angle at vertex C′ will also be θ.
θ+2β=180∘⟹β=180∘−θ2
Continuing this process, for triangle T3, the angle at the vertex opposite the base will again be θ, and the angles at the other two vertices will be γ.
θ+2γ=180∘⟹γ=180∘−θ2
We can see a pattern forming:
- For Tn, the angle at the vertex opposite the base remains θ.
- The angles at the other two vertices are given by:
Angle An=Angle Bn=180∘−θ2
As n approaches infinity, the angle θ approaches 60∘ (since the angles should sum to 180∘ and become equal). Thus, we can conclude that:
Angle An=Angle Bn=Angle Cn=60∘
Thus, we have shown that as n→∞, triangle Tn approaches an equilateral triangle.
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
- LINEAR INEQUALITIESBook:CENGAGE ENGLISHChapter:LINEAR INEQUALITIESExercise:All Questions
Explore 68 Videos
Similar Questions
Construct an isosceles triangle whose base in 8 cm and altitude 4 cm and then another triangle whose sides are 112 times the corresponding sides of the isosceles triangle.
View SolutionThe circumference of a circle circumscribing an equilateral triangle is 24πunits. Find the area of the circle inscribed in the equilateral triangle.
View Solution
Knowledge Check
Let Tn denote the number of triangles which can be be formed using the vertices of a regular polygon of n sides. If Tn+1−Tn=21, then n=
A5B7C6D4
If the vertices of a triangle having integral coordinates . Prove that triangle can't be equileteral .
View SolutionIn an equilateral triangle of side 24cm, a circle is inscribed touching its sides. Find the area of the remaining portion of the triangle (Take√3=1.732)
View SolutionIn triangle ABC, if sinAcosB=14and3tanA=tanB,thencot2A is equal to
View SolutionIn Figure, PQRS is a square and SRT is an equilateral triangle. Prove that PT=QT (ii) ∠TQR=150
View SolutionThe sides of a triangle are in A.P. and its area is 35th of the an equilateral triangle of the same perimeter, prove that its sides are in the ratio 3:5:7, and find the greatest angle of the triangle.
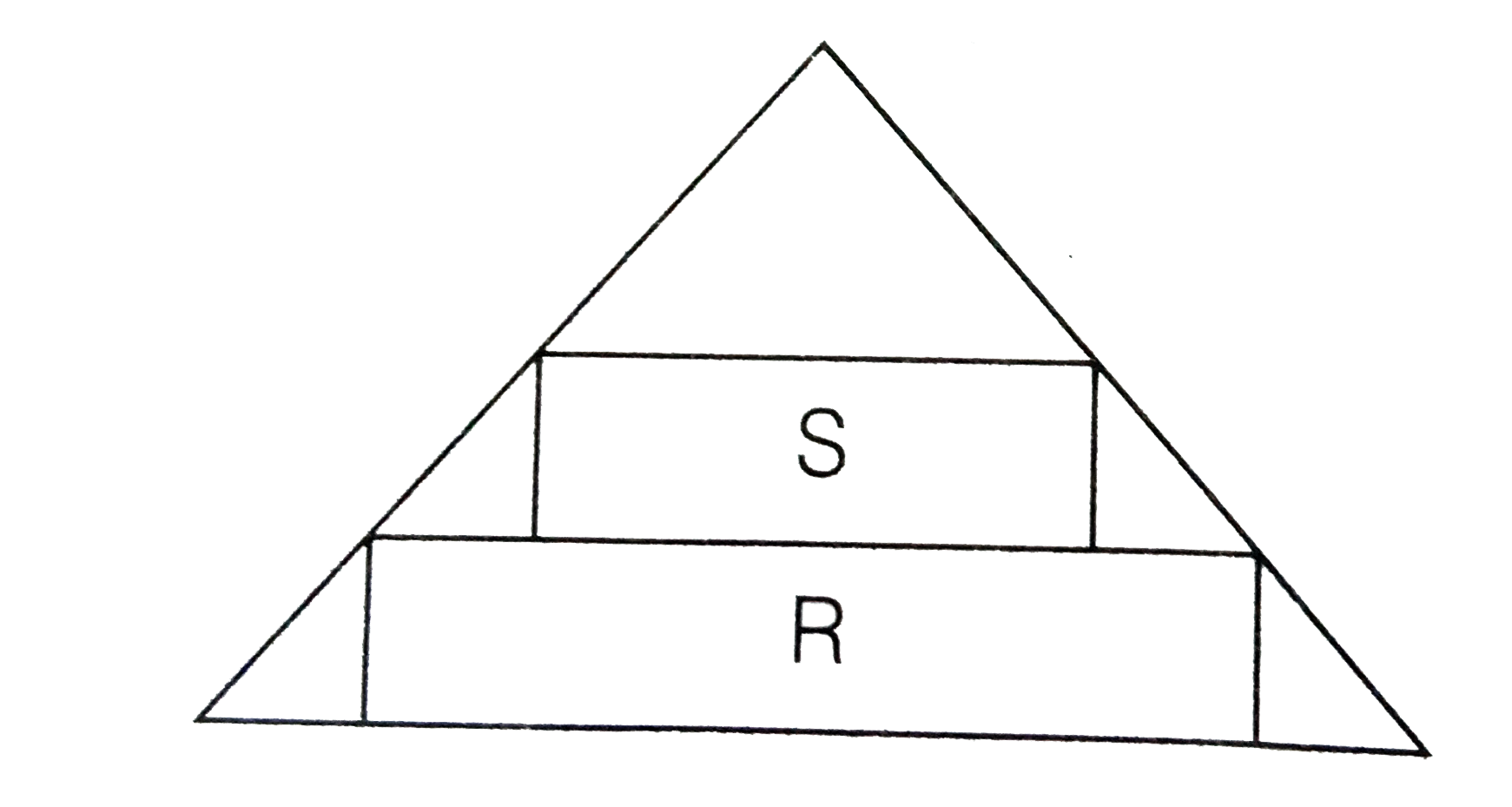
View SolutionLet T be an acute triangle Inscribe a pair R,S of rectangle in T as shown:
Let A(x) denote the area of polygon X find the maximum value (or show that no maximum exists), of A(R)+A(S)A(T), where T ranges over all triangles and R,S over all rectangle as above.
 .
.
View SolutionABCD is a square with side AB = 2. A point P moves such that its distance from A equals its distance from the line BD. The locus of P meets the line AC at T1 and the line through A parallel to BD at T2 and T3. The area of the triangle T1T2T3 is :
View Solution

