(a) Explain with reason, how the power of a diverging lens changes when (i) it is kept in a medium of refractive index greater than that of the lens, (ii) incident red light is replaced by violet light.
(b) Three lenses L1,L2,L3 each of focal length 30 cm are placed co-axially as shown in the figure. An object is held at 60 cm from the optic center of lens L1. The final real image is formal at the focus of L3. Calculate the separation between (i) (L1andL2)and (ii) (L2andL3).
Solution:
Part (a):
1. Power of a Diverging Lens in Different Media:
- The power (P) of a lens is given by the formula:
P=1f
where f is the focal length of the lens.
- For a diverging lens, the focal length f is negative.
2. Effect of a Medium with Higher Refractive Index:
- When a diverging lens is placed in a medium with a refractive index greater than that of the lens, the effective focal length changes.
- Using the lens maker's formula:
1f=(μ2μ1−1)(1r1−1r2)
where μ1 is the refractive index of the lens and μ2 is the refractive index of the medium.
- If μ2>μ1, then μ2μ1<1, making the term (μ2μ1−1) negative.
- This results in a positive focal length, meaning the diverging lens behaves like a converging lens in this medium.
3. Effect of Changing Light Color:
- The power of a lens is also dependent on the wavelength of light used.
- Red light has a longer wavelength compared to violet light.
- The refractive index μ is inversely proportional to the wavelength λ:
μ∝1λ
- Since the wavelength of violet light is shorter than that of red light, the refractive index for violet light is higher.
- Thus, replacing red light with violet light increases the power of the lens because the effective focal length decreases.
Part (b):
1. Setup of the Lenses:
- We have three lenses L1, L2, and L3, each with a focal length f=30cm.
- An object is placed at a distance of 60cm from the optic center of lens L1.
2. Finding the Image from L1:
- Using the lens formula:
1f=1v−1u
where u=−60cm (object distance is negative in lens formula).
- For lens L1:
130=1v1+160
1v1=130−160=2−160=160
v1=60cm
- Thus, the image I1 is formed at 60cm on the opposite side of L1.
3. Finding the Image from L2:
- The image I1 acts as an object for lens L2. The object distance for L2 is the distance between L1 and L2 minus 60cm.
- Let d1 be the distance between L1 and L2:
u2=d1−60
- For lens L2:
130=1v2−1(d1−60)
- Rearranging gives:
1v2=130+1(d1−60)
4. Finding the Image from L3:
- The final image is formed at the focus of L3, which is 30cm from its optic center.
- The object distance for L3 will be d2 (distance between L2 and L3) minus the image distance from L2.
5. Calculating Distances:
- Since the final image is at the focus of L3, we can set up the equations:
d1+d2=90cm
- Solving for d1 and d2 gives:
- d1=30cm
- d2=30cm
Final Answers:
- (i) The separation between L1 and L2 is 30cm.
- (ii) The separation between L2 and L3 is 30cm.
- The power (P) of a lens is given by the formula:
P=1f
where f is the focal length of the lens.
- For a diverging lens, the focal length f is negative.
- When a diverging lens is placed in a medium with a refractive index greater than that of the lens, the effective focal length changes.
- Using the lens maker's formula:
1f=(μ2μ1−1)(1r1−1r2)
where μ1 is the refractive index of the lens and μ2 is the refractive index of the medium.
- If μ2>μ1, then μ2μ1<1, making the term (μ2μ1−1) negative.
- This results in a positive focal length, meaning the diverging lens behaves like a converging lens in this medium.
- The power of a lens is also dependent on the wavelength of light used.
- Red light has a longer wavelength compared to violet light.
- The refractive index μ is inversely proportional to the wavelength λ:
μ∝1λ
- Since the wavelength of violet light is shorter than that of red light, the refractive index for violet light is higher.
- Thus, replacing red light with violet light increases the power of the lens because the effective focal length decreases.
- We have three lenses L1, L2, and L3, each with a focal length f=30cm.
- An object is placed at a distance of 60cm from the optic center of lens L1.
- Using the lens formula:
1f=1v−1u
where u=−60cm (object distance is negative in lens formula).
- For lens L1:
130=1v1+160
1v1=130−160=2−160=160
v1=60cm
- Thus, the image I1 is formed at 60cm on the opposite side of L1.
- The image I1 acts as an object for lens L2. The object distance for L2 is the distance between L1 and L2 minus 60cm.
- Let d1 be the distance between L1 and L2:
u2=d1−60
- For lens L2:
130=1v2−1(d1−60)
- Rearranging gives:
1v2=130+1(d1−60)
- The final image is formed at the focus of L3, which is 30cm from its optic center.
- The object distance for L3 will be d2 (distance between L2 and L3) minus the image distance from L2.
- Since the final image is at the focus of L3, we can set up the equations:
d1+d2=90cm
- Solving for d1 and d2 gives:
- d1=30cm
- d2=30cm
- (i) The separation between L1 and L2 is 30cm.
- (ii) The separation between L2 and L3 is 30cm.
Similar Questions
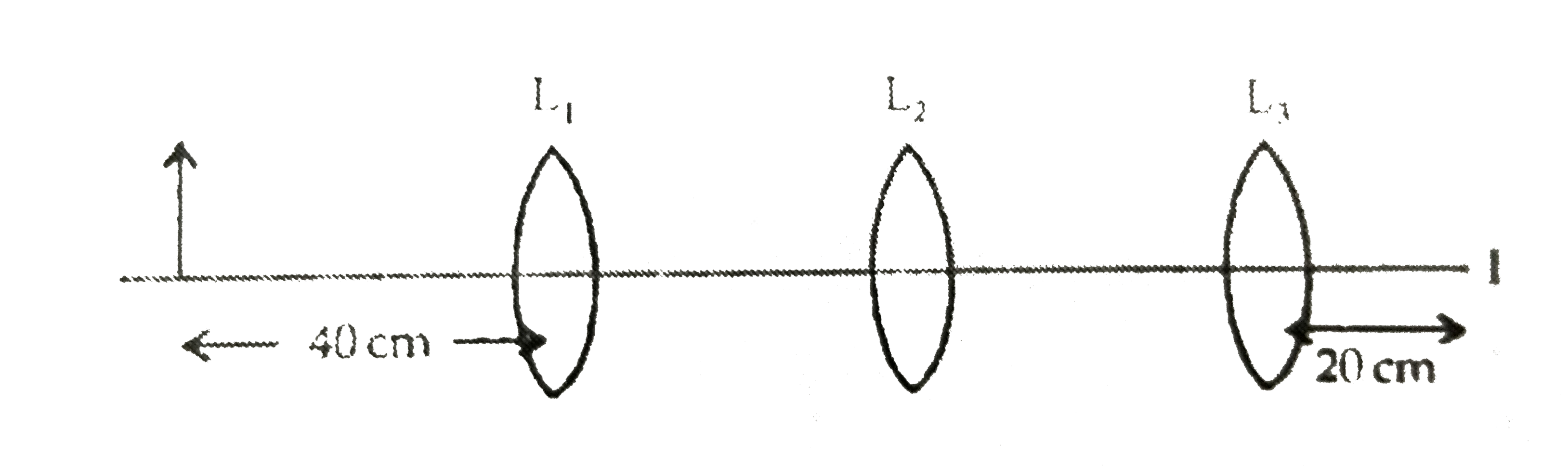
You are given three lenses L1,L2andL3 each of focal length 20 cm. An object is kept at 40 cm in front of L1, as shown. The final real image is formed at the focus 'I' of L3. Find the separations between L1,L2andL3.
View SolutionYou are given three lenses L1,L2andL3 each of focal length 10 cm. An object is kept at 15 cm in front of L1, as shown. The final real image is formed at the focus 'T' of L3. Find the separations between L1,L2andL3.
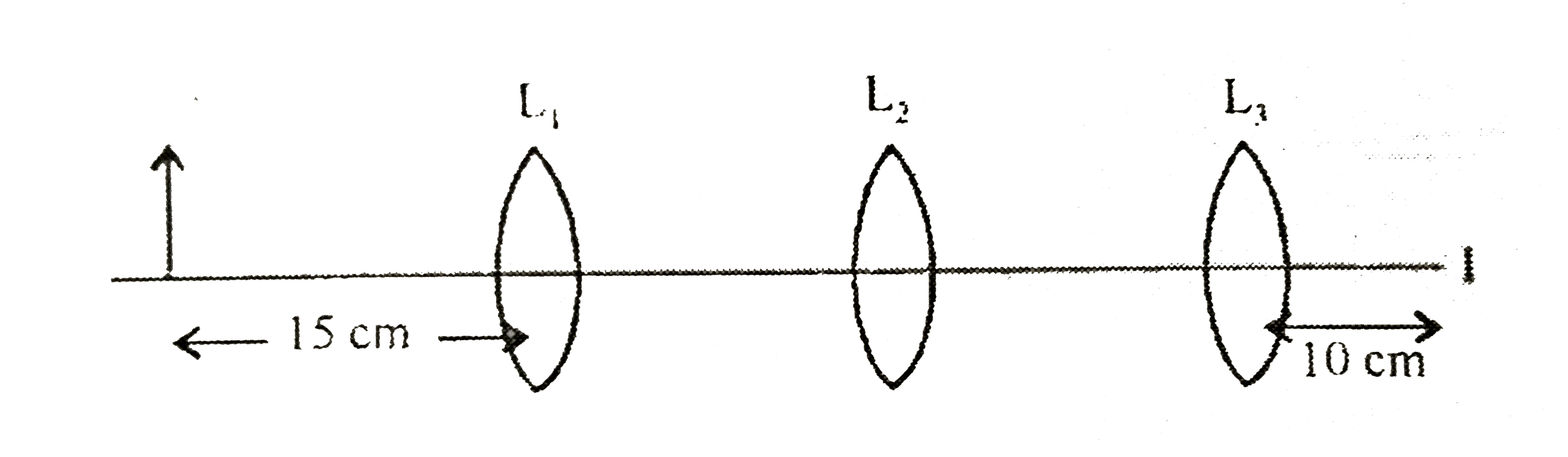
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
A convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
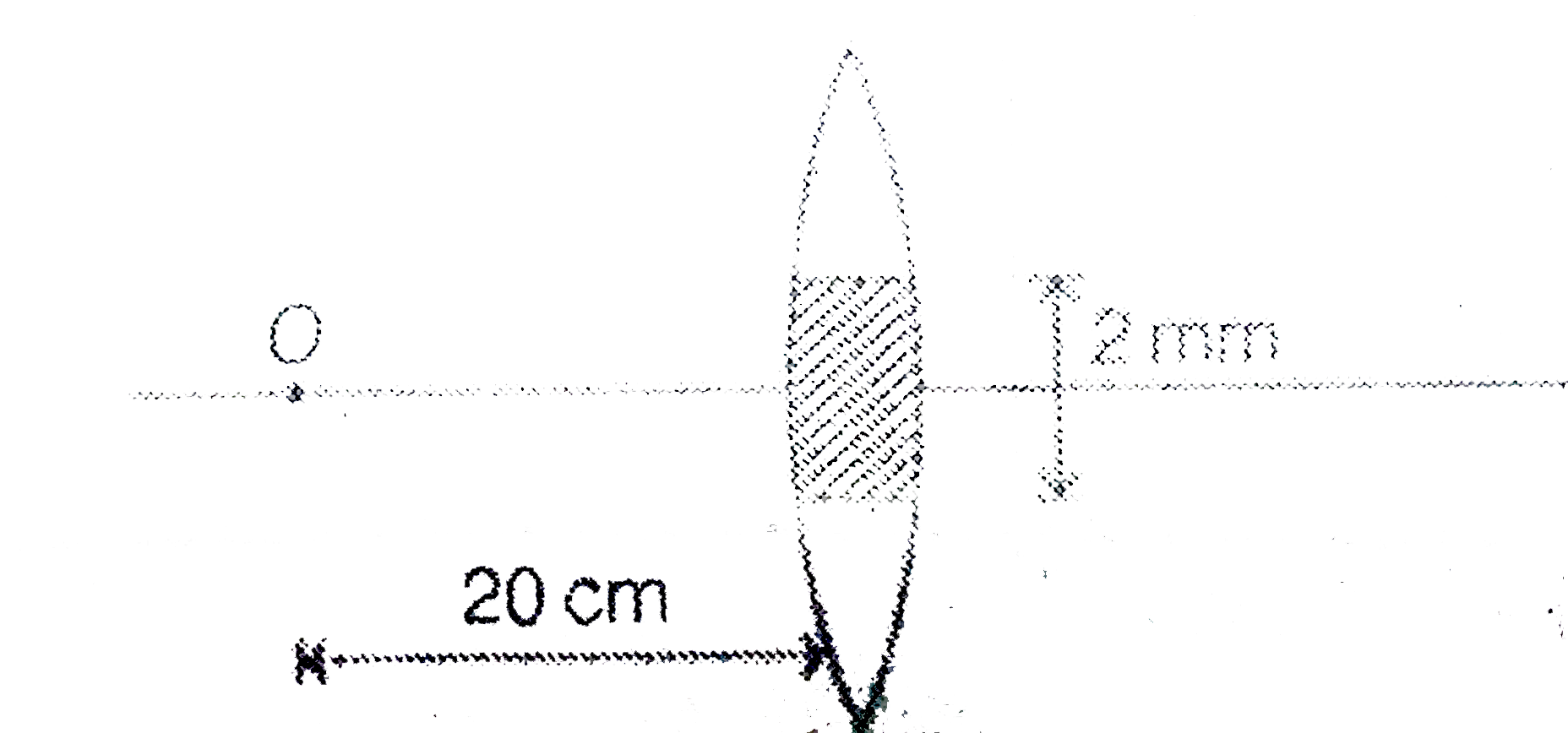
View SolutionIf a convex lens of refractive index μl is placed in a medium of refractive index μm Such that μl>μm>μair then
View SolutionAn optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
View SolutionA converging lens of refractive index 1.5 is kept in a liquid medium having the same refractive index. What would be the focal length of the lens in the medium ?
View SolutionA lens of focal length 20 cm forms an inverted image at a distance 60 cm from the lens.
(i) Identify the lens.
(ii) How far is the lens present in front of the object ?
(iii) Calculate the magnification of the image.
View SolutionAn object 15cm high is placed 10cm from the optical center of a thin lens. Its image is formed 25cm from the optical center on the same side of the lens as the object
View SolutionExplain giving reason, how the resolving power of a compound microscope depends on the
(a) frequency of the incident light, (b) focal length of the objectives lens.
View Solution
