Draw 3 equipotential surfaces corresponding to a field that uniformly increases in magnitude but remains constant along positive Z-direction. How are these surfaces different from that of a constant electric field along Z-direction ?
To solve the problem, we need to draw three equipotential surfaces corresponding to an electric field that uniformly increases in magnitude but remains constant along the positive Z-direction. We will also compare these surfaces with those of a constant electric field along the Z-direction.
1. Understand Equipotential Surfaces:
- Equipotential surfaces are defined as surfaces where the electric potential is the same at every point. This means that no work is done when moving a charge along these surfaces.
2. Set Up the Coordinate System:
- Draw a three-dimensional Cartesian coordinate system with the X-axis, Y-axis, and Z-axis. The electric field is directed along the Z-axis.
3. Draw Equipotential Surfaces for Increasing Electric Field:
- Since the electric field is increasing in magnitude along the Z-direction, we can draw three equipotential surfaces (let's label them Surface 1, Surface 2, and Surface 3).
- These surfaces will be horizontal planes parallel to the XY-plane.
- The distance between Surface 1 and Surface 2 (denote this as r1) will be greater than the distance between Surface 2 and Surface 3 (denote this as r2). This is because as we move up in the Z-direction, the electric field strength increases, leading to a decrease in the distance between equipotential surfaces.
4. Draw Equipotential Surfaces for Constant Electric Field:
- Now, draw another set of three equipotential surfaces for a constant electric field along the Z-direction.
- These surfaces will also be horizontal planes parallel to the XY-plane.
- In this case, the distances between the surfaces (r1 and r2) will be equal since the electric field strength does not change.
5. Compare the Two Scenarios:
- For the increasing electric field, the distances between the equipotential surfaces decrease (r1 > r2).
- For the constant electric field, the distances between the equipotential surfaces remain the same (r1 = r2).
Summary of Differences:
- In a uniformly increasing electric field, the equipotential surfaces get closer together as you move in the direction of the field.
- In a constant electric field, the equipotential surfaces are evenly spaced.
- Equipotential surfaces are defined as surfaces where the electric potential is the same at every point. This means that no work is done when moving a charge along these surfaces.
- Draw a three-dimensional Cartesian coordinate system with the X-axis, Y-axis, and Z-axis. The electric field is directed along the Z-axis.
- Since the electric field is increasing in magnitude along the Z-direction, we can draw three equipotential surfaces (let's label them Surface 1, Surface 2, and Surface 3).
- These surfaces will be horizontal planes parallel to the XY-plane.
- The distance between Surface 1 and Surface 2 (denote this as r1) will be greater than the distance between Surface 2 and Surface 3 (denote this as r2). This is because as we move up in the Z-direction, the electric field strength increases, leading to a decrease in the distance between equipotential surfaces.
- Now, draw another set of three equipotential surfaces for a constant electric field along the Z-direction.
- These surfaces will also be horizontal planes parallel to the XY-plane.
- In this case, the distances between the surfaces (r1 and r2) will be equal since the electric field strength does not change.
- For the increasing electric field, the distances between the equipotential surfaces decrease (r1 > r2).
- For the constant electric field, the distances between the equipotential surfaces remain the same (r1 = r2).
- In a uniformly increasing electric field, the equipotential surfaces get closer together as you move in the direction of the field.
- In a constant electric field, the equipotential surfaces are evenly spaced.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Describe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
View SolutionEquipotential surfaces associated with an electric field which is increasing in magnitude along the x-direction are
View Solution(a) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.
(b) Derive an expression for the electric potential at any point along the axial line of an electric dipole
View SolutionDefine an equipotential surface. Draw equipotential surfaces :
(i) in the case of single point charge and
(ii) in a constant electric field in Z-direction.
Why the equpotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Given reason.
View SolutionEquipotential surfaces associated with a uniform electric field along positive x-axis are planes parallel to
View SolutionSome equipotential surfaces are shown in figure(29.E3) What can you say about the magnitude and the direction of the electric field?

View SolutionIf the given figure shows equipotential surfaces, then the magnitude of electric field is
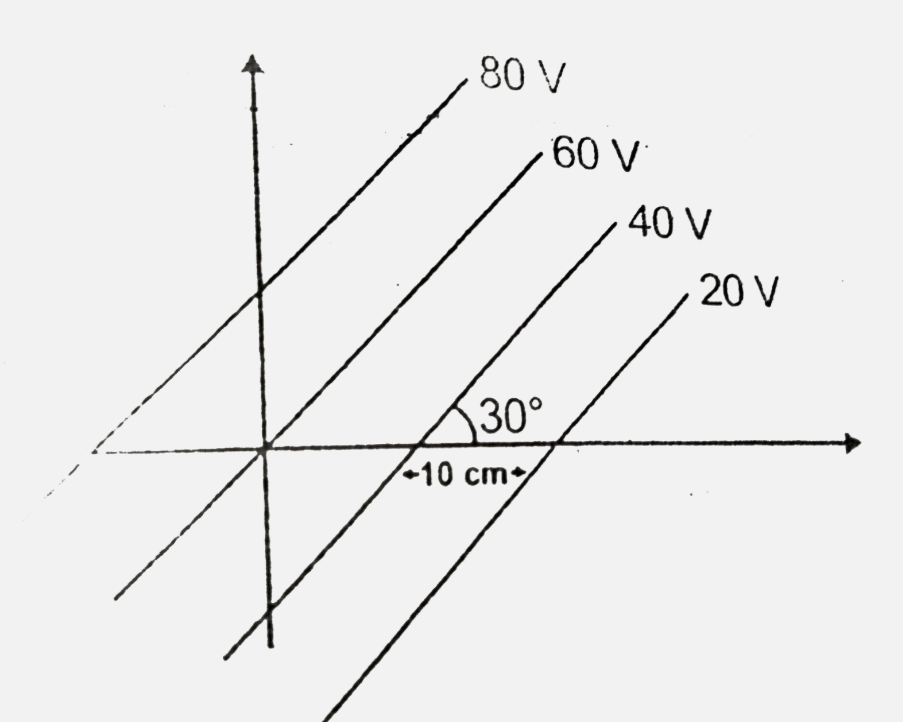
View SolutionThree equipotential surfaces are shown in (Fig. 3.28) A. Draw the corresponding field lines and estimate the field strength at a point A where the distance between the surfaces is 4 cm.
a.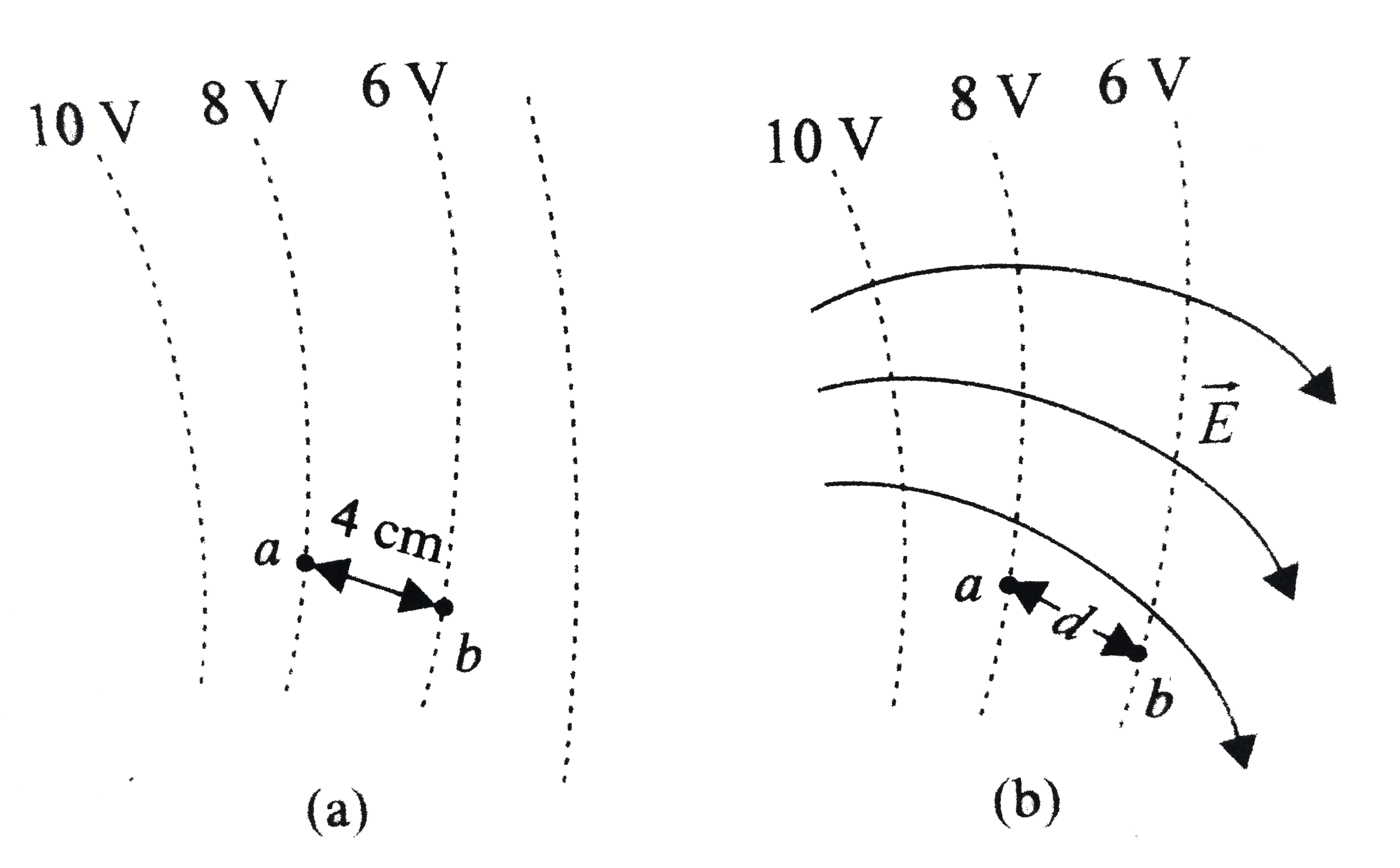
View SolutionA family of equipotential surface are shown. The direction of the electric field at point A is along-

View SolutionFigure shows equipotential surfaces concentric at O the magnitude of electric field at a distance r measured from O is
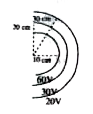
View Solution
