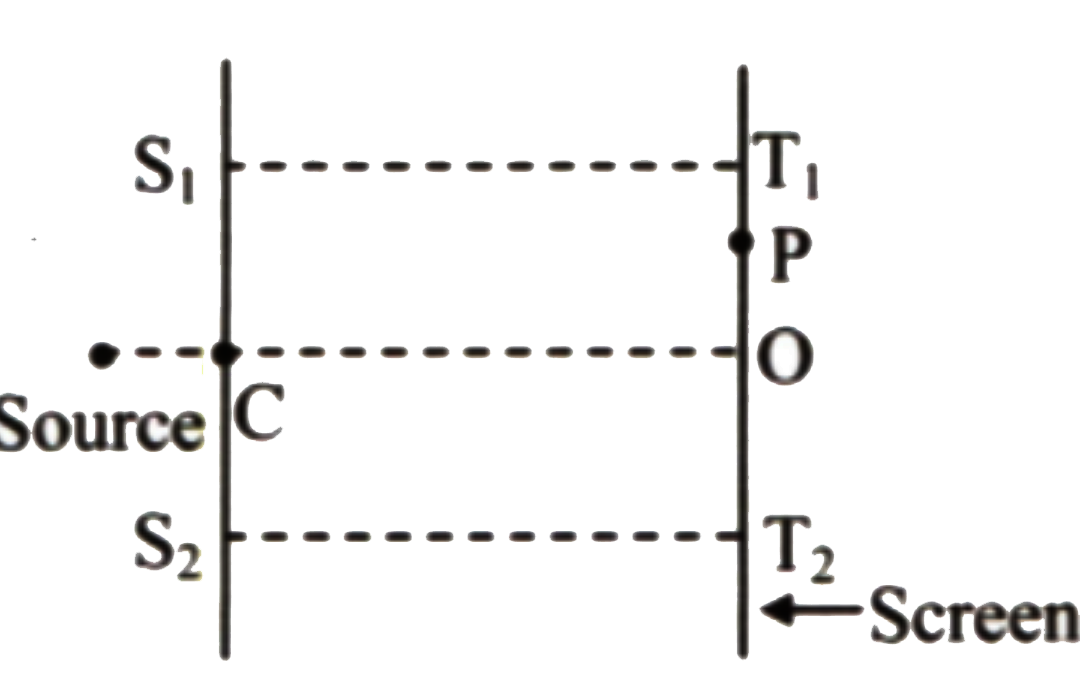
Consider a two slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of such that the first minima on the screen falls at a distance D from the centre O.

From the given figure of two slit interference arrangements, we can write
and
and
The minima will occur when
i.e., [for first minima n=1]
If x=D
we can write
Putting
Topper's Solved these Questions
- WAVE OPTICSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Long Answer type Questions
5 Videos
- WAVE OPTICSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Very short Answer Type Questions.
6 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITEXERCISE - Multiplel choice questions
26 Videos
Similar Questions
Consider a two slit interference arrangements such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.

View SolutionIn a special arrangement of Young's double - slits d is twice the distance between the screen and the slits D, i.e. d = 2D. For the setup, the value of D such that the first minima on the screen fall at a distance D from the centre O is found to be λN, where λ is the wavelength of light used. What is the value of N ? [Take √5=2.24]
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionA beam of light consisting of two wavelenths, 6500 Å and 5200 Å is used to obtain interference fringes in a Young's double slit experiment (1Å=10−10m). The distance between the slits is 2.0 mm and the distance between the plane of the slits and the screen in 120 cm. (a) Find the distance of the third bright frings on the screen from the central maximum for the wavelength 6500 Å (b) What is the least distance from the central maximum where the bright frings due to both the wavlelengths coincide ?
View SolutionIn young's double slit experiment, distance between the slit S1andS2 is d and the distance between slit and screen is D . Then longest wavelength that will be missing on the screen in front of S1 is
View SolutionIn Young's double slit experiment, if the distance between two slits is equal to the wavelength of used light. Then the maximum number of bright firnges obtained on the screen will be
View SolutionIn a double slit experiment ,the separation between the slits is d=0.25cm and the distance of the screen D=100cm from the slits .if the wavelength of light used in λ=6000Åand I0is the intensity of the central bright fringe. The intensity at a distance x=4×10−5in form the central maximum is-
View Solution
