An electron and a position are released from (0, 0, 0) and (0,0,1⋅5R) respectively, in a uniform magnetic field →B=B0ˆi, each with an equal momentum of magnitude p=eBR. Under what conditions on the direction of momentum will the orbits be non-intersecting circles?
To solve the problem, we need to determine the conditions under which the orbits of an electron and a positron, released from different points in a uniform magnetic field, do not intersect.
1. Understanding the Setup:
- The electron is released from the origin (0, 0, 0).
- The positron is released from the point (0, 0, 1.5R).
- Both particles have equal momentum p=eBR and experience a magnetic field →B=B0^i.
2. Direction of Momentum:
- Let the momentum of the electron make an angle θ with the y-axis. Thus, the momentum vector can be represented as:
→pe=p(sinθ^j+cosθ^k)
- Similarly, for the positron, let its momentum make an angle θ with the y-axis but in the opposite direction:
→pp=p(−sinθ^j+cosθ^k)
3. Radius of Circular Motion:
- Both particles will move in circular paths due to the magnetic force acting on them. The radius of their circular paths is R.
4. Finding the Centers of the Orbits:
- The center of the electron's circular path can be represented as:
Ce=(0,Rsinθ,Rcosθ)
- The center of the positron's circular path can be represented as:
Cp=(0,−Rsinθ,1.5R−Rcosθ)
5. Distance Between the Centers:
- The distance d between the centers Ce and Cp can be calculated using the distance formula:
d=√(0−0)2+(Rsinθ−(−Rsinθ))2+(Rcosθ−(1.5R−Rcosθ))2
- Simplifying this, we find:
d=√(2Rsinθ)2+(2Rcosθ−1.5R)2
- This simplifies to:
d=√4R2sin2θ+(Rcosθ−1.5R)2
6. Condition for Non-Intersecting Orbits:
- For the orbits to be non-intersecting, the distance d must be greater than the sum of the radii of the two orbits (which is 2R):
d>2R
- Squaring both sides gives:
d2>4R2
7. Substituting for d2:
- Substitute the expression for d2 into the inequality:
4R2sin2θ+(Rcosθ−1.5R)2>4R2
- Simplifying this leads to:
4R2sin2θ+R2(cosθ−1.5)2>4R2
8. Final Condition:
- After simplifying the above inequality, we arrive at:
94>6cosθ
- Thus, we find:
cosθ<38
Conclusion:
The condition for the orbits of the electron and positron to be non-intersecting circles is:
cosθ>38
- The electron is released from the origin (0, 0, 0).
- The positron is released from the point (0, 0, 1.5R).
- Both particles have equal momentum p=eBR and experience a magnetic field →B=B0^i.
- Let the momentum of the electron make an angle θ with the y-axis. Thus, the momentum vector can be represented as:
→pe=p(sinθ^j+cosθ^k)
- Similarly, for the positron, let its momentum make an angle θ with the y-axis but in the opposite direction:
→pp=p(−sinθ^j+cosθ^k)
- Both particles will move in circular paths due to the magnetic force acting on them. The radius of their circular paths is R.
- The center of the electron's circular path can be represented as:
Ce=(0,Rsinθ,Rcosθ)
- The center of the positron's circular path can be represented as:
Cp=(0,−Rsinθ,1.5R−Rcosθ)
- The distance d between the centers Ce and Cp can be calculated using the distance formula:
d=√(0−0)2+(Rsinθ−(−Rsinθ))2+(Rcosθ−(1.5R−Rcosθ))2
- Simplifying this, we find:
d=√(2Rsinθ)2+(2Rcosθ−1.5R)2
- This simplifies to:
d=√4R2sin2θ+(Rcosθ−1.5R)2
- For the orbits to be non-intersecting, the distance d must be greater than the sum of the radii of the two orbits (which is 2R):
d>2R
- Squaring both sides gives:
d2>4R2
- Substitute the expression for d2 into the inequality:
4R2sin2θ+(Rcosθ−1.5R)2>4R2
- Simplifying this leads to:
4R2sin2θ+R2(cosθ−1.5)2>4R2
- After simplifying the above inequality, we arrive at:
94>6cosθ
- Thus, we find:
cosθ<38
The condition for the orbits of the electron and positron to be non-intersecting circles is:
cosθ>38
Topper's Solved these Questions
- MOVING CHARNGES AND MAGNETISMBook:NCERT EXEMPLAR ENGLISHChapter:MOVING CHARNGES AND MAGNETISMExercise:Short Answer Type Question
Explore 6 Videos
- MAGNETISM AND MATTER Book:NCERT EXEMPLAR ENGLISHChapter:MAGNETISM AND MATTER Exercise:All Questions
Explore 24 Videos
- NUCLEIBook:NCERT EXEMPLAR ENGLISHChapter:NUCLEIExercise:Long answer type question
Explore 10 Videos
Similar Questions
Knowledge Check
An electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
Aremains constantBincreases with timeCdecreases with timeDincreases and decreases periodically
A charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=B0ˆj. Then it's de-Broglie wavelength
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
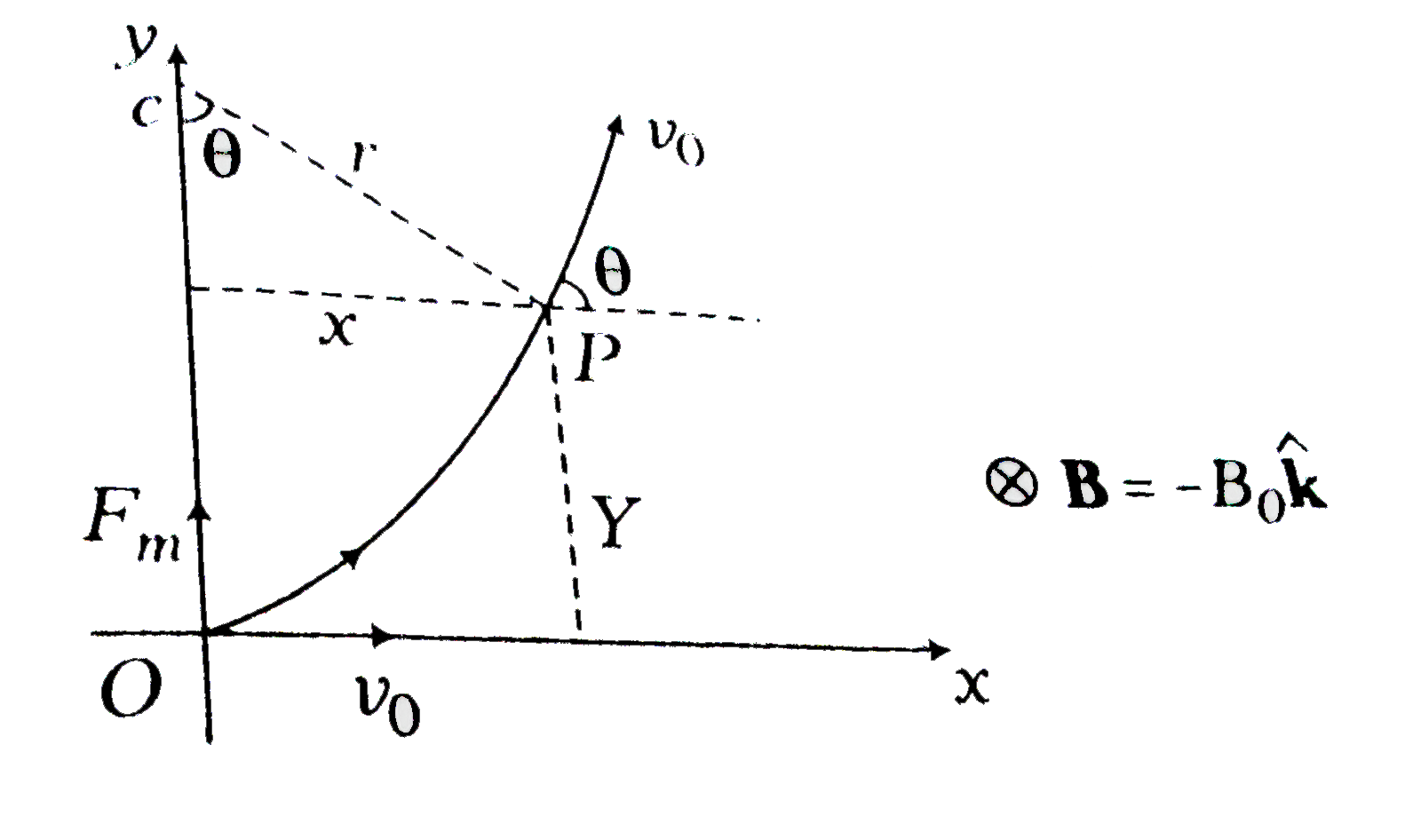
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View SolutionA particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.

View SolutionA particle of specific charge α starts moving from (0,0,0) under the action of electric field E=eˆi and magnetic field →B=B0ˆk. Its velocity at (x, 0, 0) is 4ˆi+3ˆj. Find the value of x
View SolutionUnder what condition is E∘cell=0 or ΔrG=0?
View Solution

