Bohr.s theory explains that when Hydrogen-like particles are excited, their electrons are shifted higher energy orbits. As such a state of atom is not stable, electrons return to lower energy orbits releasing quantum of energy. Thus different spectral lines are formed. The wave number of spectral line is given by ¯v=2π2me4z2ch3⎡⎢
⎢⎣1n21−1n22⎤⎥
⎥⎦
For a hydrogen -like particle, ionization energy is 122.4 eV. Then what is the wave number of series limit spectral line of the particle of paschen seres (R = rydberg.s constant)Solution in Telugu
R9
R3
R
4R
The correct Answer is:C
Step by step video, text & image solution for Bohr.s theory explains that when Hydrogen-like particles are excited, their electrons are shifted higher energy orbits. As such a state of atom is not stable, electrons return to lower energy orbits releasing quantum of energy. Thus different spectral lines are formed. The wave number of spectral line is given by bar(v) = (2pi^(2)me^(4)z^(2))/(c h^(3))[(1)/(n_(1)^(2)-(1)/(n_(2)^(2)))] For a hydrogen -like particle, ionization energy is 122.4 eV. Then what is the wave number of series limit spectral line of the particle of paschen seres (R = rydberg.s constant) by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - AAKASH SERIESCHAPTER - ATOMIC STRUCTUREEXERCISE - Level - II (Type-I) (Practice sheet - 6 (Section -C : Matching/Straight objective type questions))
2 Videos
- ATOMIC STRUCTUREBOOK - AAKASH SERIESCHAPTER - ATOMIC STRUCTUREEXERCISE - Level-II (Type - II) (Lecture sheet - 1 (subjective/Analytical type Questions))
8 Videos
- ATOMIC STRUCTUREBOOK - AAKASH SERIESCHAPTER - ATOMIC STRUCTUREEXERCISE - Level - II (Type-I) (Practice sheet - 6 (Section-A : More than one correct answer type questions))
5 Videos
- AROMATIC HYDROCARBONSBOOK - AAKASH SERIESCHAPTER - AROMATIC HYDROCARBONSEXERCISE - OBJECTIVE EXERCIES - 3 (RECENT AIPMT/NEET QUESTIONS)
10 Videos
- CHEMICAL BONDINGBOOK - AAKASH SERIESCHAPTER - CHEMICAL BONDINGEXERCISE - OBJECTIVE EXERCISE -3 (RECENT AIPMT/NEET QUESTIONS )
39 Videos
Similar Questions
Match the following columns

View SolutionMass numbers of Li, Be and B are 7, 9 and 10 respectively. Among B+,Be2+,Li+, Be Which has two electrons, three protons and four neutrons
View SolutionThe nucleus of an atom is located at x = y = z = 0. If the probability of finding an s orbital electron in a tiny volume around x=a, y=z=0 is 1.×10−5, choose the correct statements(s) regarding the probability of electron
View SolutionUsing anhydrous AICI3 as catalyst which one of the following reactions produces ethyl benzene
View SolutionIn which of the following pairs, the two species are isostructural?
View SolutionThe wavelength of the spectral line when the electron is the hydrogen atom undergoes a transition from the energy level 4 to energy level 2 is.
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure). Maximum number of different lines produced when electron jump from nth level to ground level is equal to (n(n-1))/(2). For example in the case of n=4, number of lines produced is 6.(4to3,4to2,4to1,3to2,3to1,2to1). When an electron returns from n_(2) "to"n_(1) state, the number of different lines in the spectrum will be equal to ((n_(2)-n_(1))(n_(2)-n_(1)+1))/(2) If the electron comes back from energy level having energy E_(2) to energy level having energy E_(1), then the difference may be expressed in terms of energy of photon as: E_(2)-E_(1)=DeltaE,lambda=(hc)/(DeltaE),DeltaE=hv(v-"frequency") Since h and c are constants DeltaE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom. Wave number of line is given by the formula: barv=RZ^(2)((1)/(n_(1)^(2))-(1)/(n_(2)^(2))) where R is a Rydberg constant (R=1.1xx10^(7)m^(-1)). (i) First line of a series : It is called line of longest wavelength of line of smallest energy'. (ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy. Last line of breakett series for H-atom has wavelength lambda_(1)"Å" and 2nd line of Lyman series has wavelength lambda_(2)"Å" then:
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
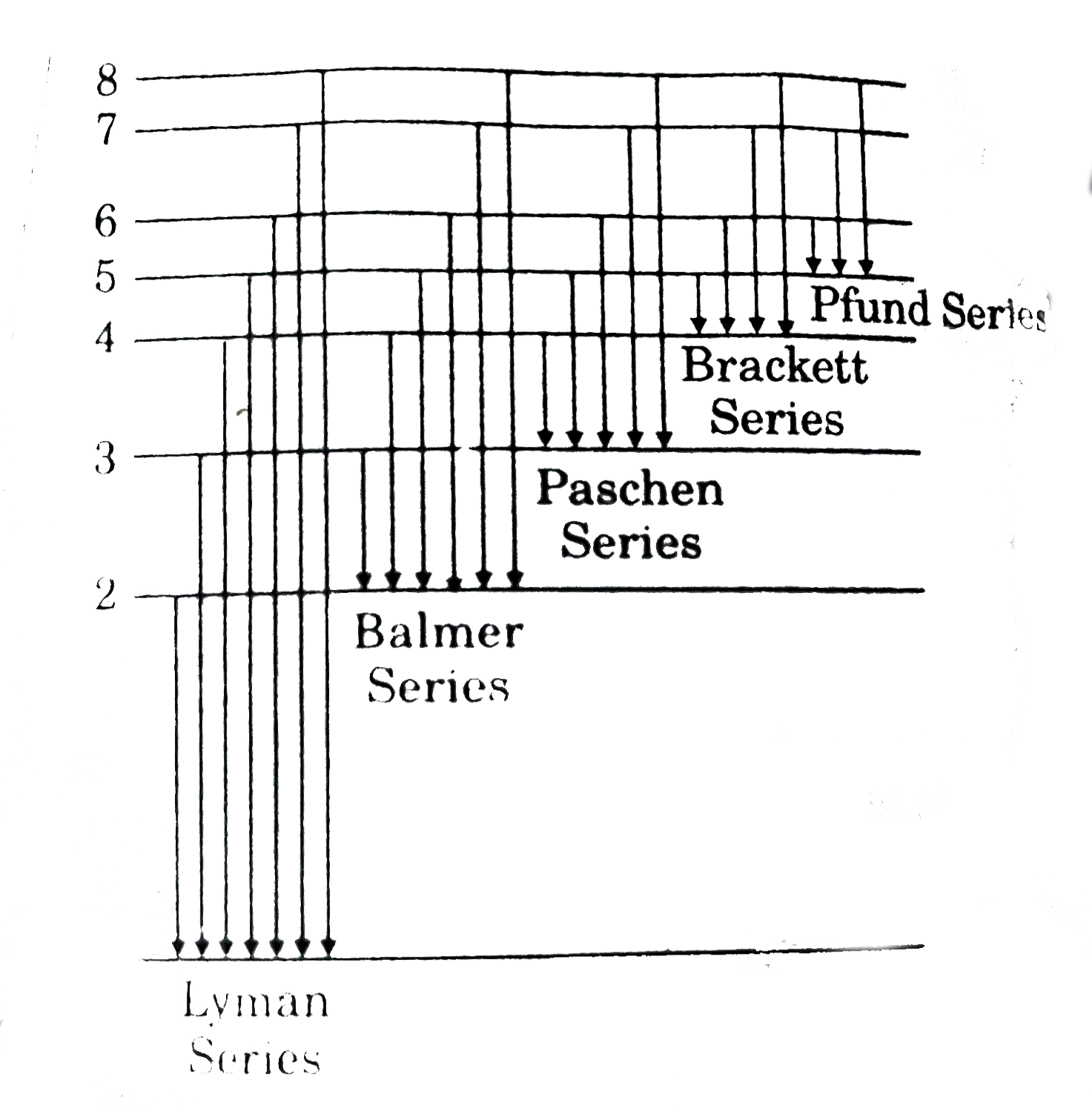
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
wave number of the first line of Paschen series in Be3+ ion is :
View SolutionOne of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n=1 orbit, the orbit in which it has the lowest energy. When the electon is in this lowest energy orbit, the atom is said to be in its ground electronic state. If the atom receives energy from an outside source, it is possible for the electron to move ot an orbit with a higher n value, in which case the atoms is in an excited state with a higher energy.
The law of conservation of energy says that we cannot create or destroy energy. Thus, if a certain amount of external energy is required to excite an electron from one energy level to another, then that same amount of energy will be liberated when the electron returns to its initial state.
Lyman series is observed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electrons returns to the third, fourth and fifth orbits from higher energy orbits respectively.
When electrons return form n2 to n1 state, the number of lines in the spectrum will equal to
(n2−n1)(n2−n1+1)2
If the electon comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as :
E2−E1=ΔE,δE⇒hcλ
Since, h and c are constant, δE corresponds to definite energy. Thus, each transition from one energy level to another will produce a radiatiob of definite wavelength. This is actually Wave number of a spectral line is given by the formula
¯v=R(1n21−1n22).
where R is a Rydberg's constant (R=1.1×107m−1)
If the wavelength of series limit of Lyman series for He+ ion is x Å, then what will be the wavelength of series limit of Balmer series for Li2+ ion?
View SolutionOne of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n=1 orbit, the orbit in which it has the lowest energy. When the electon is in this lowest energy orbit, the atom is said to be in its ground electronic state. If the atom receives energy from an outside source, it is possible for the electron to move ot an orbit with a higher n value, in which case the atoms is in an excited state with a higher energy. The law of conservation of energy says that we cannot create or destroy energy. Thus, if a certain amount of external energy is required to excite an electron from one energy level to another, then that same amount of energy will be liberated when the electron returns to its initial state. Lyman series is observed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electrons returns to the third, fourth and fifth orbits from higher energy orbits respectively. When electrons return form n_(2) " to " n_(1) state, the number of lines in the spectrum will equal to ((n_(2)-n_(1))(n_(2)-n_(1)+1))/(2) If the electon comes back from energy level having energy E_(2) to energy level having energy E_(1) , then the difference may be expressed in terms of energy of photon as : E_(2)-E_(1)=DeltaE, deltaE implies (hc)/(lambda) Since, h and c are constant, deltaE corresponds to definite energy. Thus, each transition from one energy level to another will produce a radiatiob of definite wavelength. This is actually Wave number of a spectral line is given by the formula barv=R((1)/(n_(1)^(2))-(1)/(n_(2)^(2))) . where R is a Rydberg's constant (R=1.1xx10^(7) m^(-1)) The emission spectra is observed by the consequence of transition of electrons from higher energy state to ground state of He^(+) ion. Six different photons are observed during the emission spectra, then what will be the minimum wavelength during the transition?
View SolutionOne of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n=1 orbit, the orbit in which it has the lowest energy. When the electon is in this lowest energy orbit, the atom is said to be in its ground electronic state. If the atom receives energy from an outside source, it is possible for the electron to move ot an orbit with a higher n value, in which case the atoms is in an excited state with a higher energy. The law of conservation of energy says that we cannot create or destroy energy. Thus, if a certain amount of external energy is required to excite an electron from one energy level to another, then that same amount of energy will be liberated when the electron returns to its initial state. Lyman series is observed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electrons returns to the third, fourth and fifth orbits from higher energy orbits respectively. When electrons return form n_(2) " to " n_(1) state, the number of lines in the spectrum will equal to ((n_(2)-n_(1))(n_(2)-n_(1)+1))/(2) If the electon comes back from energy level having energy E_(2) to energy level having energy E_(1) , then the difference may be expressed in terms of energy of photon as : E_(2)-E_(1)=DeltaE, deltaE implies (hc)/(lambda) Since, h and c are constant, deltaE corresponds to definite energy. Thus, each transition from one energy level to another will produce a radiatiob of definite wavelength. This is actually Wave number of a spectral line is given by the formula barv=R((1)/(n_(1)^(2))-(1)/(n_(2)^(2))) . where R is a Rydberg's constant (R=1.1xx10^(7) m^(-1)) What transition in the hydrogen spectrum would have the same wavelength as Balmer transitio, n=4 " to "n=2 in the He^(+) spectrum?
View SolutionOne of the fundamental laws of physics is that matter is most stable with the lowest possible energy. Thus, the electron in a hydrogen atom usually moves in the n=1 orbit, the orbit in which it has the lowest energy. When the electon is in this lowest energy orbit, the atom is said to be in its ground electronic state. If the atom receives energy from an outside source, it is possible for the electron to move ot an orbit with a higher n value, in which case the atoms is in an excited state with a higher energy. The law of conservation of energy says that we cannot create or destroy energy. Thus, if a certain amount of external energy is required to excite an electron from one energy level to another, then that same amount of energy will be liberated when the electron returns to its initial state. Lyman series is observed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electrons returns to the third, fourth and fifth orbits from higher energy orbits respectively. When electrons return form n_(2) " to " n_(1) state, the number of lines in the spectrum will equal to ((n_(2)-n_(1))(n_(2)-n_(1)+1))/(2) If the electon comes back from energy level having energy E_(2) to energy level having energy E_(1) , then the difference may be expressed in terms of energy of photon as : E_(2)-E_(1)=DeltaE, deltaE implies (hc)/(lambda) Since, h and c are constant, deltaE corresponds to definite energy. Thus, each transition from one energy level to another will produce a radiatiob of definite wavelength. This is actually Wave number of a spectral line is given by the formula barv=R((1)/(n_(1)^(2))-(1)/(n_(2)^(2))) . where R is a Rydberg's constant (R=1.1xx10^(7) m^(-1)) An electron in H-atom in M-shell on de-excitation to ground state gives maximum ........... spectrum lines.
View SolutionHydrogen atom: The electronic ground state of hydrogen atom contains one electron in the first orbit. If sufficient energy is provided, this electron can be promoted to higher energy levels. The electronic energy of a hydrogen-like species (any atom//ions with nuclear charge Z and one electron) can be given as E_(n)=-(R_(H)Z^(2))/(n^(2)) where R_(H)= "Rydberg constant," n= "principal quantum number" The energy required to promote the ground state electron of H-atom to the first excited state is: When an electron returns from a higher energy level to a lower energy level, energy is given out in the form of UV//Visible radiation.
View SolutionHydrogen atom: The electronic ground state of hydrogen atom contains one electron in the first orbit. If sufficient energy is provided, this electron can be promoted to higher energy levels. The electronic energy of a hydrogen-like species (any atom//ions with nuclear charge Z and one electron) can be given as E_(n)=-(R_(H)Z^(2))/(n^(2)) where R_(H)= "Rydberg constant," n= "principal quantum number" A gaseous excited hydrogen-like species with nuclear charge Z can emit radiations of six different photon energies. (a) The principal quantum number of the excited state is : (b) It was observed that when this excited species emits photons of energy =2.64 eV when it comes to next lower energy state. Calculate the nuclear charge of the species. The least energy required to remove an electron from a species is know as the ionization energy (I.E.) of the species. The experimental I.E. of He atom is 24.58 eV .
View Solutionएक हाइड्रोजन-सदृश परमाणु की n वी कक्षा में इलेक्ट्रॉन की ऊर्जा En=−xn2eV है। परमाणु की आयनन ऊर्जा लिखिये।
View Solution
