A student obtained the following marks per centage in an examination English - 50, Accounts - 75, Economics - 60, B Std.-80, Hindi - 55. If weights are 2, 3, 3, 2, 1, respectively allotted to the subjects, his weighted mean is
50+75+60+80+552+3+3+2+1
(50×2)+(75×3)+(60×3)+(80×2)+(55×1)5
50×2+75×3+60×3+80×+55×12+3+3+2+1
none
The correct Answer is:C
To find the weighted mean of the student's marks, we will follow these steps:
Step 1: List the Marks and Weights
We have the following marks and their corresponding weights:
- English: Marks = 50, Weight = 2
- Accounts: Marks = 75, Weight = 3
- Economics: Marks = 60, Weight = 3
- B Std.: Marks = 80, Weight = 2
- Hindi: Marks = 55, Weight = 1
Step 2: Calculate the Weighted Marks
Next, we will multiply each subject's marks by its corresponding weight:
- Weighted Marks for English = 50 × 2 = 100
- Weighted Marks for Accounts = 75 × 3 = 225
- Weighted Marks for Economics = 60 × 3 = 180
- Weighted Marks for B Std. = 80 × 2 = 160
- Weighted Marks for Hindi = 55 × 1 = 55
Step 3: Sum of Weighted Marks
Now, we will sum all the weighted marks calculated in the previous step:
Total Weighted Marks = 100 + 225 + 180 + 160 + 55 = 720
Step 4: Sum of Weights
Next, we will sum the weights:
Total Weights = 2 + 3 + 3 + 2 + 1 = 11
Step 5: Calculate the Weighted Mean
Finally, we will calculate the weighted mean using the formula:
Weighted Mean=Total Weighted MarksTotal Weights=72011≈65.45
Thus, the weighted mean of the student's marks is approximately 65.45.
---
We have the following marks and their corresponding weights:
- Accounts: Marks = 75, Weight = 3
- Economics: Marks = 60, Weight = 3
- B Std.: Marks = 80, Weight = 2
- Hindi: Marks = 55, Weight = 1
Next, we will multiply each subject's marks by its corresponding weight:
- Weighted Marks for Accounts = 75 × 3 = 225
- Weighted Marks for Economics = 60 × 3 = 180
- Weighted Marks for B Std. = 80 × 2 = 160
- Weighted Marks for Hindi = 55 × 1 = 55
Now, we will sum all the weighted marks calculated in the previous step:
Next, we will sum the weights:
Finally, we will calculate the weighted mean using the formula:
Topper's Solved these Questions
Similar Questions
A student obtained the following marks in percentages in his semester examination English 50, Maths 65, Statistics 70, Economics 58 and Accountancy 63. The weights of these subjects are 2, 2, 1, 1 and 1 respectively. What is the weighted arithmetic mean? (a) 60 (b) 61 (c) 62 (d) 63
View SolutionA student obtains the following percentage in an examination.
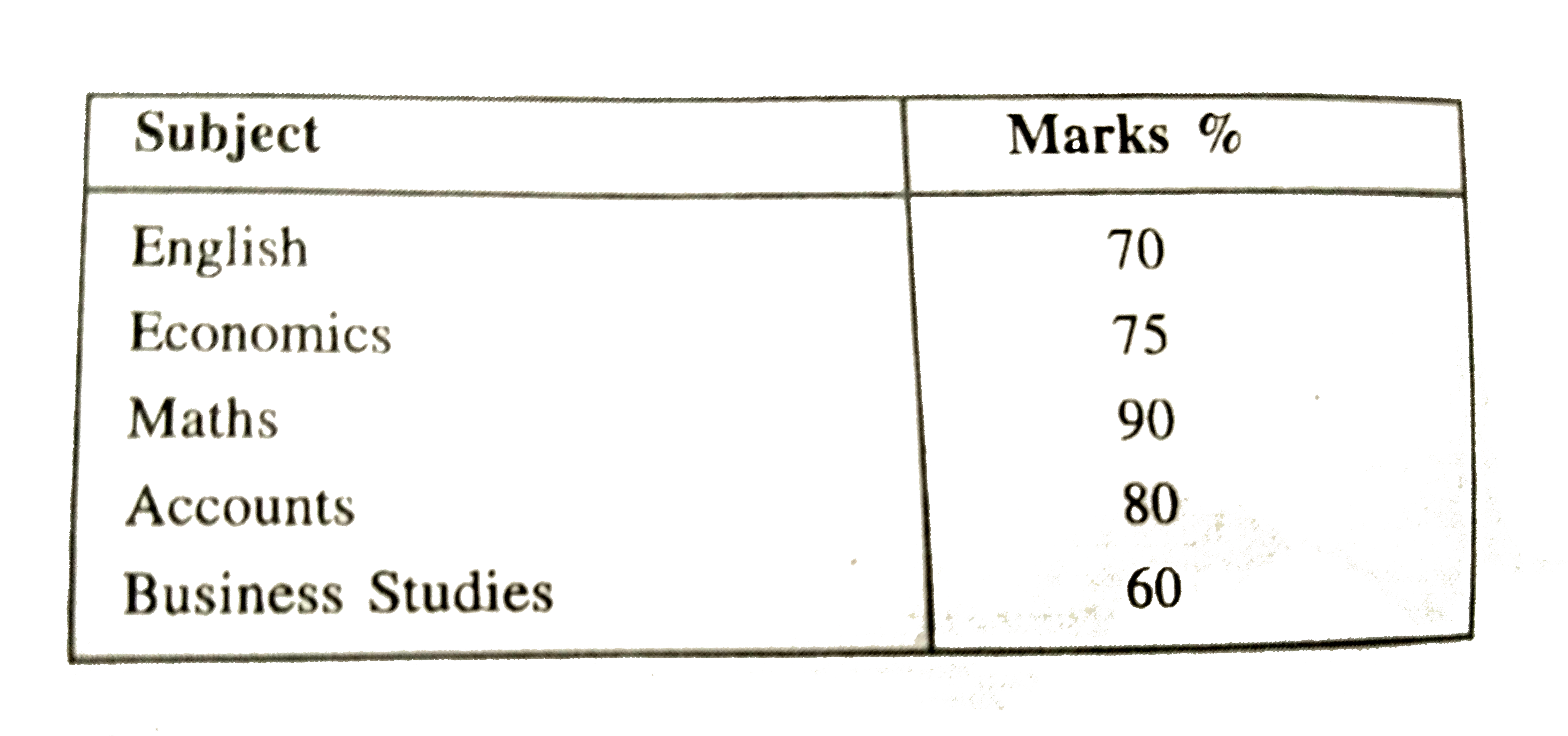
(i) Find out simple mean marks , if all subjectes are given equal weight.
(ii) Find out weighted mean marks, if the respective weights are 1,2,1,2,3
View Solution
Knowledge Check
A candidate obtained the following percentage of marks in an examination English 60, Maths 90, Physics 75, Chemistry 66. If weighs 2, 4, 3, 3 are allotted to these subjects respectively, then the weight mean is given by
A60+90+75+662+4+3+3B60×2+90×4+75×3+66×32+4+3+3C60×2+90×4+75×3+66×34D60+90+75+664A candidate obtains the marks in subjects, English 40, Hindi 30, Mathematics 60, Physics 70 and Chemistry 40. In the weights of 1, 2, 2, 3, 3 respectively are allotted to the subjects, then in the candidates weighted mean is
A59B615C10D50In an examination, a candidate scores the following percentage of marks. English-44, Hindi-58, Maths—74, Physics-61, Chemistry—62. If weights 2, 4, 4, 5, 3 respectively, are allotted to these subjects, then the candidate's weighted mean percentage is
A61B61.5C62D62.5
A student obtained 60 marks in English, 75 in Hindi, 63 in Mathematics, 59 in Economics and 55 in Statistics. Calculate weighted mean of the marks if weights are respectively 2, 1, 5, 5 and 3.
View SolutionA student obtained 60 marks in English, 75 in Hindi, 63 in Mathematics, 59 in Economics and 55 in Statistics. Calculate weighted mean of the marks if weights are respectively 2, 1, 5, 5 and 3.
View SolutionA student obtained 60, 75 and 85 marks respectively in three monthly examinations in Physics and 95 marks in the final examination. The three monthly examinations are of equal weightage whereas the final examination is weighted twice as much as a monthly examination. His average marks in Physics are (a) 78.75 (b) 79 (c) 82 (d) 85
View SolutionA college student has to appear for two examinations A and B. The probabilities that the student passes in A and B are 2/3 and 3/4 respectively. If it is known that the student passes at least one among the two examinations, then the probability that the student will pass both the examination is (A) 1/6 (B) 1/2 (C) 1/3 (D) 6/11
View SolutionA candidate obtains the marks in subjects English 60 Hindi 75 , Mathematics 63 , Physics 59 and Chemistry 55 . In the weights of 1,2,1,3,3 respectively are alloted to the subjects then the candidates weighted mean is
View Solution
