Question

Find the area of region $\{(x,y):0\le y\le x^2+1,0\le y\le x+1,0\le x\le 2\}$.

Explanation

Let R ` = {(x,y) : 0 le y le (x^(2) + 1) , 0 le y le (x + 1) , 0 le x le 2}`
`= {(x,y) : 0 le y le (x^(2) + 1) } cap {(x,y) : 0 le y le ( x +1)} cap {(x,y) : 0 le x le 2}`
` = R_(1) cap R_(2) cap R_(3)`.
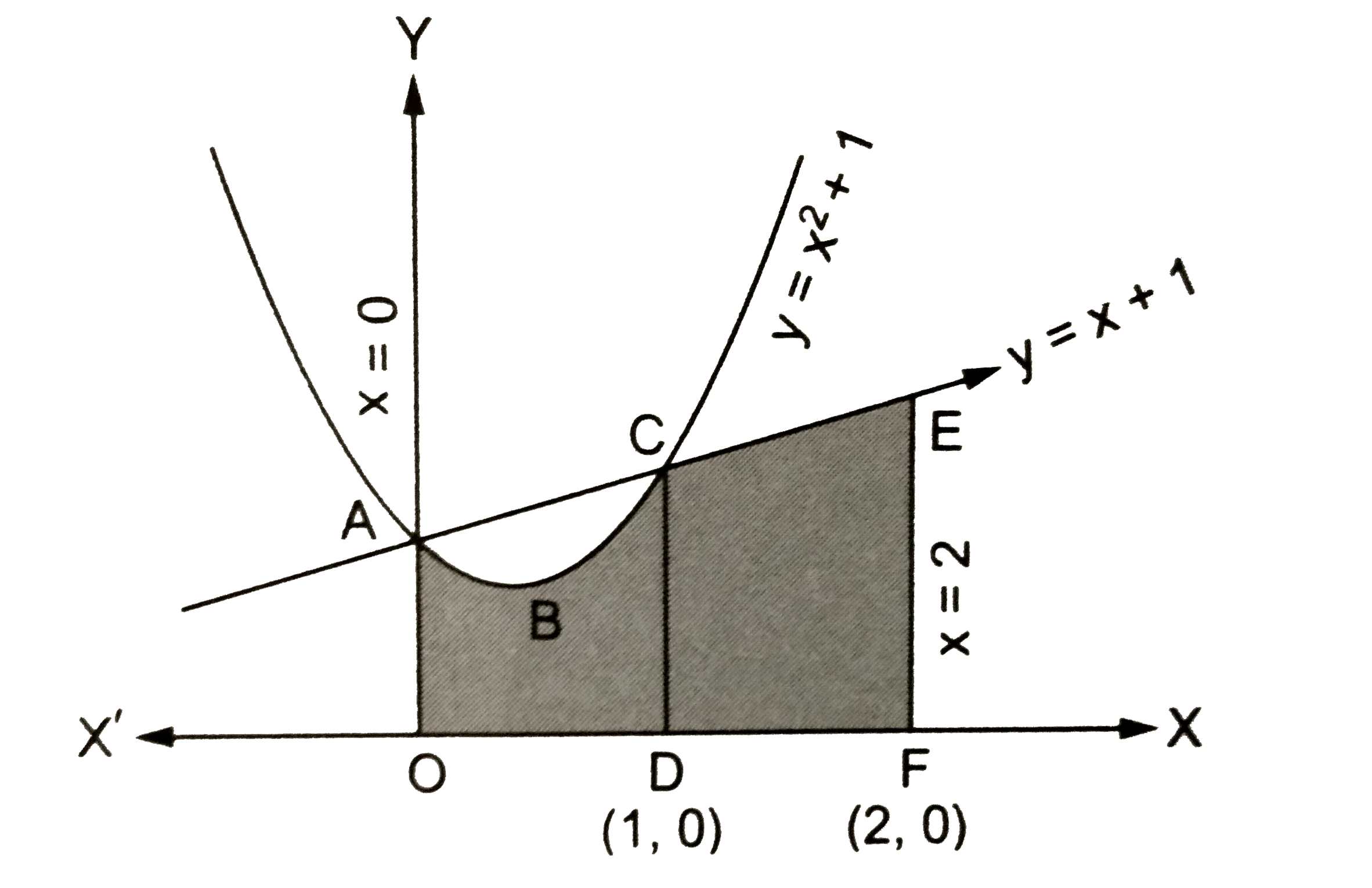
Clearly , `R_(1)` is the region consisting of the right-hand side of the y-axis , lying below the parabola `y = x^(2) + 1`.
Also ,` R_(2)` is the region consisting of the right-hand side of the y-axis , lying below the line y = (x + 1)
And `R_(3)` is the region above the axis , lying between the ordinates x = 0 and x = 2
Thus `R_(1) cap R_(2) cap R_(2) cap R_(3)` is the shaded region .

We have , `y = x^(2) + 1` and y = x + 1
`implies x^(2) + 1 = x + 1 implies x(x - 1) = 0 implies x = 0 ` or x = 1
Now , `(x = 0 implies y = 1)` and `(x = 1 implies y = 2)`.
Thus , the parabola `y = (x^(2) + 1)` and the line y = x + 1 intersect at the points A (0,1) and C(1,2) .
`therefore ` required area = area of the shaded region
= (area ODCBA) + (area CDFEC)
= `overset(1)underset(0)(int)` (y of the parabola ) dx + `overset(2) underset(1)(int)`(y of the line ) dx
`= overset(1) underset(0)int (x^(2) + 1) dx + overset(2)underset(1)(int)(x+1)dx`
`= [(x^(3))/(3) + x]_(0)^(1) + [(x^(2))/(2) + x]_(1)^(2)`
`=((1)/(3) + 1) + (4 - (3)/(2)) = (23)/(6)` sq units .
Hence the required area is `(23)/(6)` sq units