Find the area bounded by the curve $y = sin x$ between $x = 0$ and $x = 2 π$ .

Video Solution

Text Solution

Verified by Experts

The given curve is $y = sin x$
Some values of x and the corresponding values of y are given below :

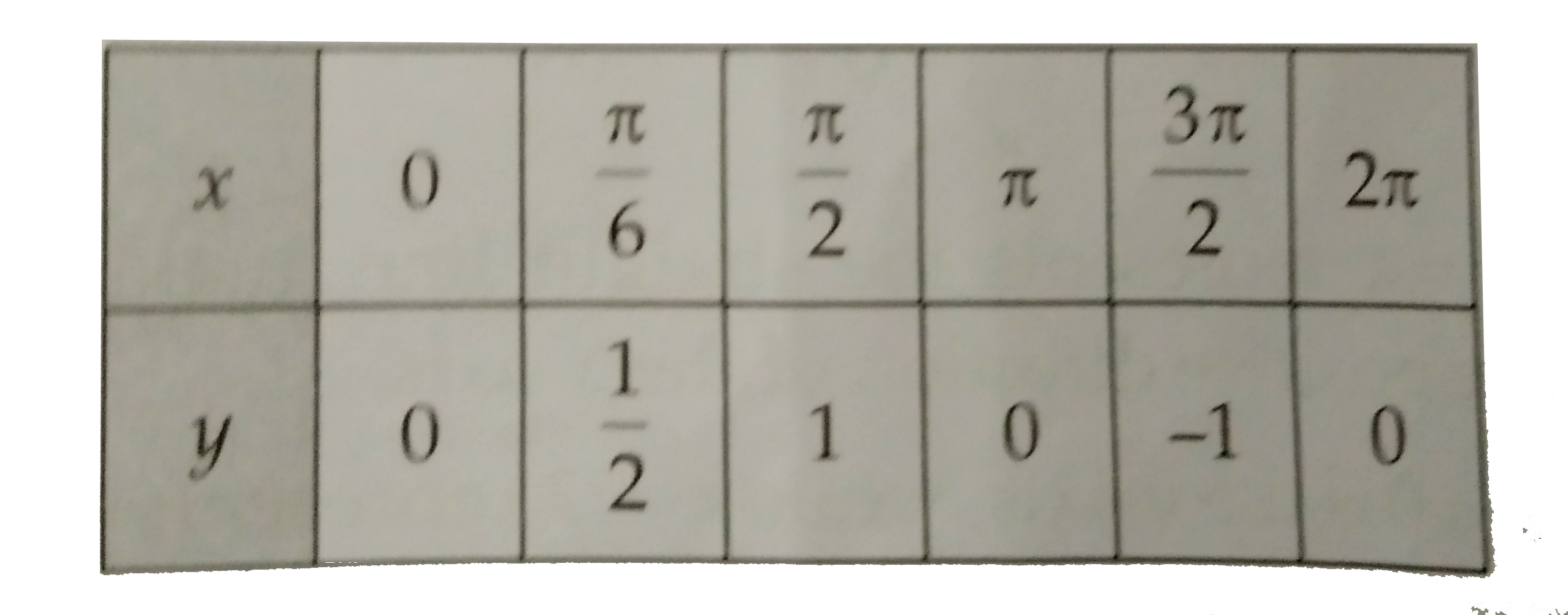
Taking a fixed unit (distance ) lfor $π$ along the x-axis , we can plot the points $(0, 0) (\frac{π}{6}, \frac{1}{2}), (\frac{π}{2}, 1), (π, 0) (3 \frac{π}{2}, - 1) and (2 π, 0)$
Join these points freehand to obtain a rough sketch of the given curve.

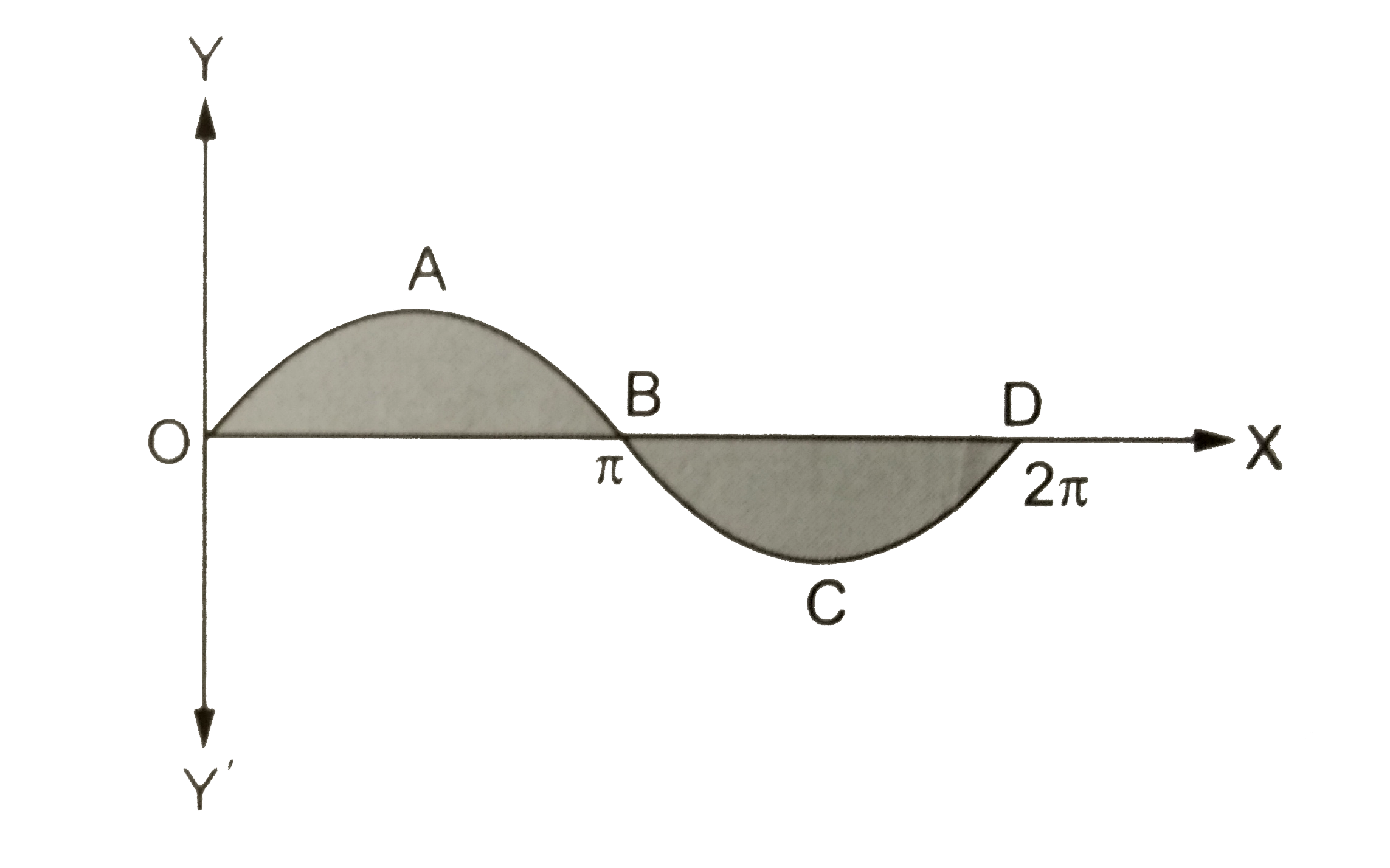
Required area = (area OABO ) + (area BCDB)
$= π \int 0 y$ dx + $2 π \int π (- y) d x [∵$ area BCDB is below the x-axis ]
$= π \int 0 sin x d x - 2 π \int π sin x d x$
$= {[- cos x]}_{0}^{π} - {[- cos x]}_{π}^{2 π} = (2 + 2) = 4$ sq units
Hence , the required area is 4 sq units.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Area bounded by the curves $y = x sin x and$ x-axis between $x = 0 and x = 2 π$ is
A $2 π$
B $3 π$
C $4 π$
DNone

RS AGGARWAL-AREA OF BOUNDED REGIONS -Exercise 17

Home
Ask Doubt
Profile