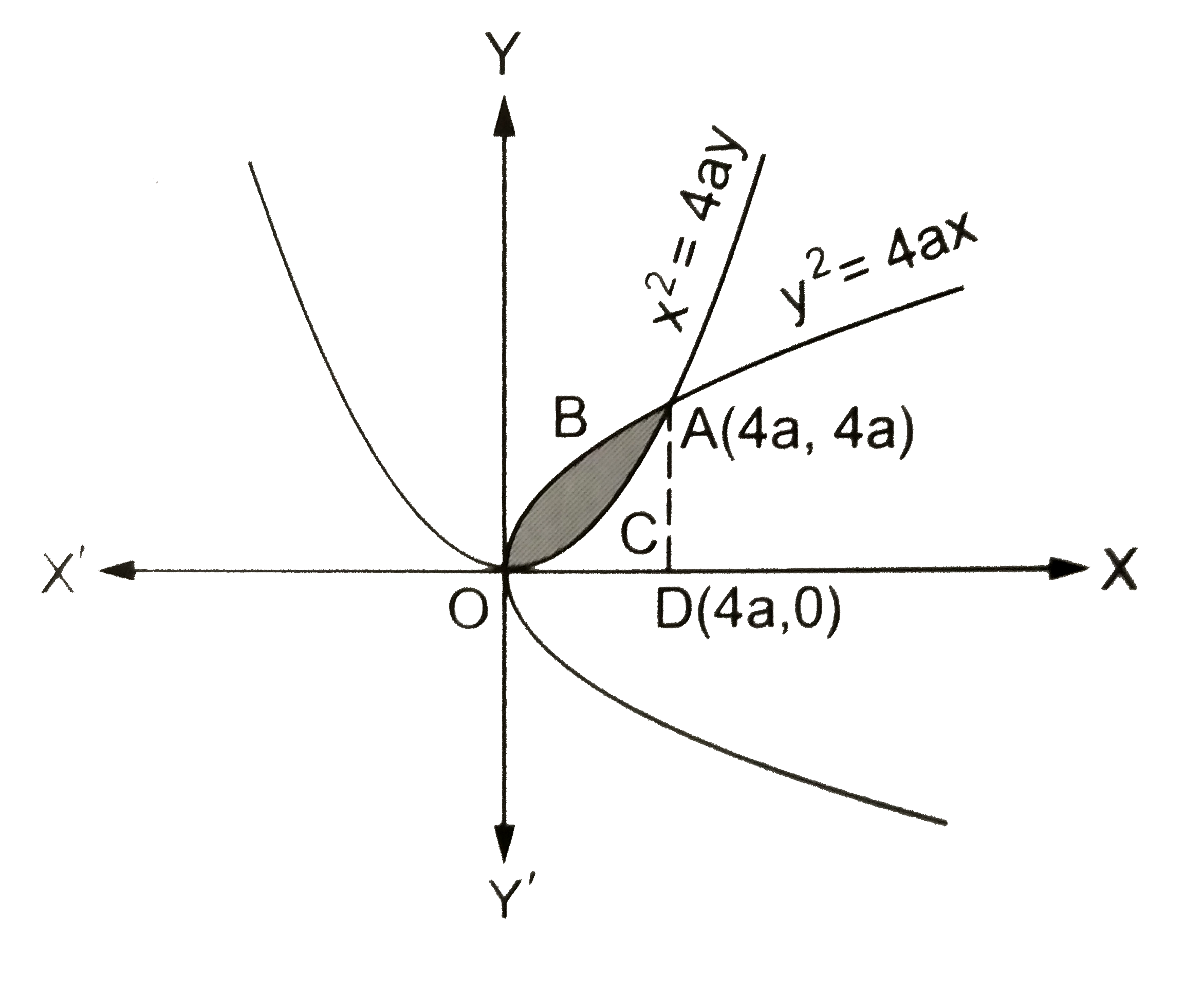
Find the area of the region included between the parabolas $y^{2} = 4 a x$ and $x^{2} = 4 a y$ , where $a > 0 .$

Video Solution

Text Solution

Verified by Experts

The given parabolas are
$y^{2} = 4 a x (i)$
and $x^{2} = 4 a y \dots . (i i)$
In order to find the points of intersection of the given curves , we slove (i) and (ii) simulataneously .
Putting $x = \frac{y^{2}}{4} a$ from (i) in (ii)
we get $\frac{y^{4}}{16} a^{2} = 4 a y \Rightarrow y^{4} - 64 a^{3} y = 0$
$\Rightarrow y (y^{3} - 64 a^{3}) = 0$
$\Rightarrow y = 0 or y = 4 a$
Now $(y = 0 \Rightarrow x = 0) and (y = 4 a \Rightarrow x = \frac{16 a^{2}}{4 a}) = 4 a$ s
Now $(y = 0 \Rightarrow x = 0) and (y = 4 a \Rightarrow x = \frac{16 a^{2}}{4 a})$
Thus dthe points of intersection of the two parabolas are O(0,0) and A (4a, 4a) Draw $A D ⊥ O X .$ Then, point D is (4a, 0)
Required area= area OCABO
$= 4 a \int 0 y d x f or (y^{2} = 4 a x) - 4 a \int 0 y d x f or (x^{2} = 4 a y)$
$= 4 a \int 0 2 \sqrt{a x} d x - 4 a \int 0 \frac{x^{2}}{4 a} d x$
$= {[2 \sqrt{a}, \frac{2}{3} . x^{3 / 2}]}_{0}^{3 / 2} - \frac{1}{4 a} {[\frac{x^{3}}{3}]}_{0}^{4 a}$
$= [\frac{4 \sqrt{a}}{3} . {(4 a)}^{3 / 2} - \frac{1}{12 a} \times 64 a^{3}]$
$(\frac{32 a^{2}}{3} - \frac{16 a^{2}}{3}) = (\frac{16 a^{2}}{3})$ sq units
Hence, the required area is $(\frac{16 a^{2}}{3})$ sq units

Updated on:21/07/2023

The area included between the parabolas $y^{2} = 4 x and x^{2} = 4 y$ is
A $\frac{8}{3} sq. units$
B $8 sq. units$
C $\frac{16}{3} sq. units$
D $12 sq. units$
The area included between the parabolas $y^{2} = 4 a x and x^{2} = 4 b y$ is
A $\frac{8}{3} a b$
B $\frac{16}{3} a b$
C $\frac{4}{3} a b$
DNone