If O is the origin anf An is the point with coordinates (n,n+1) then (OA1)2+(OA2)2+…..+(OA7)2 is equal to
The correct Answer is:343
To solve the problem, we need to calculate the sum of the squares of the distances from the origin O(0,0) to the points An(n,n+1) for n=1 to 7.
1. Identify the Coordinates:
The coordinates of the points An are given by An(n,n+1). Thus, we have:
- A1(1,2)
- A2(2,3)
- A3(3,4)
- A4(4,5)
- A5(5,6)
- A6(6,7)
- A7(7,8)
2. Calculate the Distance Squared:
The distance from the origin O(0,0) to a point An(x,y) is given by the formula:
OA2n=x2+y2
For each An:
- OA21=12+22=1+4=5
- OA22=22+32=4+9=13
- OA23=32+42=9+16=25
- OA24=42+52=16+25=41
- OA25=52+62=25+36=61
- OA26=62+72=36+49=85
- OA27=72+82=49+64=113
3. Sum the Distances Squared:
Now, we need to sum these values:
OA21+OA22+OA23+OA24+OA25+OA26+OA27=5+13+25+41+61+85+113
4. Calculate the Total:
Performing the addition step-by-step:
- 5+13=18
- 18+25=43
- 43+41=84
- 84+61=145
- 145+85=230
- 230+113=343
5. Final Result:
Therefore, the value of (OA1)2+(OA2)2+…+(OA7)2 is 343.
Summary:
The final answer is:
343
The coordinates of the points An are given by An(n,n+1). Thus, we have:
- A1(1,2)
- A2(2,3)
- A3(3,4)
- A4(4,5)
- A5(5,6)
- A6(6,7)
- A7(7,8)
The distance from the origin O(0,0) to a point An(x,y) is given by the formula:
OA2n=x2+y2
For each An:
- OA21=12+22=1+4=5
- OA22=22+32=4+9=13
- OA23=32+42=9+16=25
- OA24=42+52=16+25=41
- OA25=52+62=25+36=61
- OA26=62+72=36+49=85
- OA27=72+82=49+64=113
Now, we need to sum these values:
OA21+OA22+OA23+OA24+OA25+OA26+OA27=5+13+25+41+61+85+113
Performing the addition step-by-step:
- 5+13=18
- 18+25=43
- 43+41=84
- 84+61=145
- 145+85=230
- 230+113=343
Therefore, the value of (OA1)2+(OA2)2+…+(OA7)2 is 343.
The final answer is:
343
Topper's Solved these Questions
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (CONCEPT - BASED) SINGLE CORRECT ANSWER TYPE QUESTIONS
15 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (LEVEL 1) SINGLE CORRECT ANSWER TYPE QUESTIONS
60 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - SOLVED EXAMPLES (LEVEL 2) SINGLE CORRECT ANSWER TYPE QUESTIONS
30 Videos
- AREA BY INTEGRATIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - AREA BY INTEGRATIONEXERCISE - Question from Previous Years. B-Architecture Entrance Examination Papers
12 Videos
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
17 Videos
Similar Questions
If the line y=3x meets the lines x=1,x=2……….,x=12 at points A1,A2…….A12 respectively then (OA1)2,+(OA1)2+....+(OA12)2 is equal to ___________.
View SolutionIf A1,A2......An are points on the line y=x lying in the positive quadrant such that OAn=n.OAn−1,O being the origin. If OA1=1 then the co-ordinates of A8 are (3a√2,3a√2,) where a is equal to
View Solution
Knowledge Check
If (a1+ib2)(a2+ib2)...(an+ibn)=A+iB, then (a21+b21)(a22+b22)...(a2n+b2n) is equal to
A1BA2+B2CA + BD1A2+1B2A and B are two points on the hyperbola O is the centre. If OA is perpendicular to OB then 1(OA)2+1(OB)2 is equal to
A1a2+1b2B1a2−1b2C1b2−1a2Da2+b2Let A (a,b) be a fixed point and O be the origin of coordionates. If A1 is the mid-point of OA, A2 is the mid- poind of AA1,A3 is the mid-point of AA2 and so on. Then the coordinates of An are
A(a(1−2−n),b(1−2−n))B(a(2n−1−1),b(2−n−1))C(a(1−2(n−1)),b(1−2(n−1)))Dnone of these
The co-ordinates of a point An is (n,n,√n) where n∈ N, If O(0,0) then 12∑i=1(OAi)2 equals _________.
View SolutionIf O is the origin and the coordinates of A and B are (51, 65) and (75, 81), respectively. Then OA×OBcos∠AOB is equal to
View SolutionFor every interger n, a line Ln is drawn through the point Pn(n,n+1) perpendicular to the line x−y+1=0 meeting x-axis at An and y-axis at Bn. If O is the origin then 10∑n=0(OAn+OBn) is equal to
View SolutionIf O be origin and A is a point on the locus y2=8x .find the locus of the middle point of OA
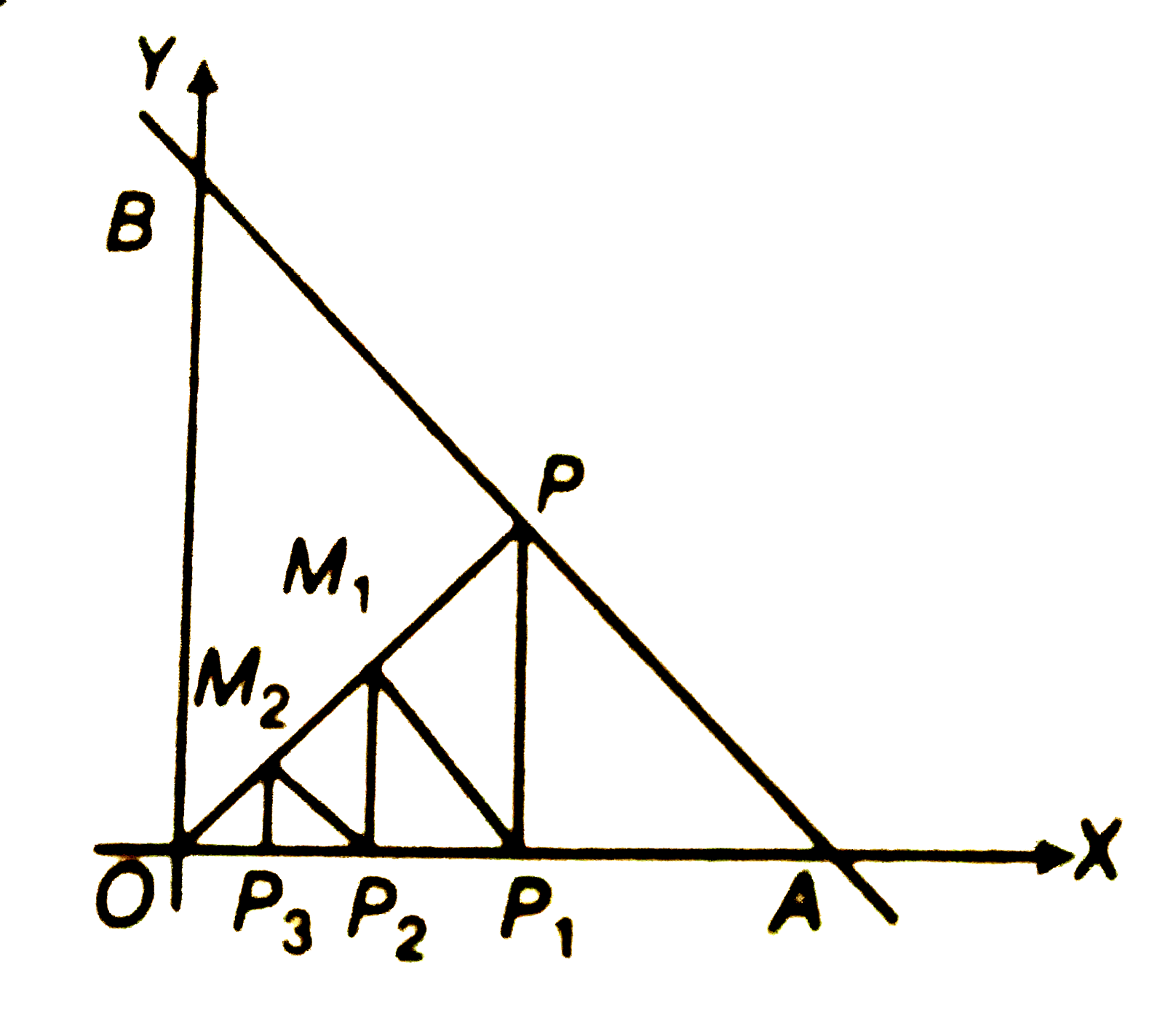
View SolutionThe line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P1 is the foot of perpendicular from P to OA,M1 is that of P1 from OP,P2 is that of M1 from OA,M2 is that of P2 from OP,P3 is that of M2 from OA and so on. If Pn denotes theb nth foot of the perpendicular on OA, then find OPn
 .
.
View Solution
