तीन कार्नो इंजन श्रेणीक्रम में तापमान के एक गर्म ऊजा भण्डार तथा T1 तापमान के एक ठण्डे ऊष्मा भण्डार के बीच लगे हैं (चित्र देखिये) । चित्रानुसार दिखाये अनुसारा T2 तथा T3तापमान के दो और ऊष्मा भण्डार है यहाँ T1>T2>T3>T4 हैं। तीनों इंजन बराबर क्षमता के होंगे, यदि
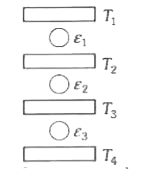
T2=(T1T24)1/3 , T3=(T21T4)1/3
T2=(T1T4)1/2 , T3=(T21T4)1/3
T2=(T31T4)1/4 , T3=(T1T34)1/4
T2=(T21T4)1/3 , T3=(T1T24)1/3
The correct Answer is:D
Step by step video, text & image solution for तीन कार्नो इंजन श्रेणीक्रम में तापमान के एक गर्म ऊजा भण्डार तथा T_(1) तापमान के एक ठण्डे ऊष्मा भण्डार के बीच लगे हैं (चित्र देखिये) । चित्रानुसार दिखाये अनुसारा T_(2) तथा T_(3)तापमान के दो और ऊष्मा भण्डार है यहाँ T_(1) gt T_(2) gt T_(3) gt T_(4) हैं। तीनों इंजन बराबर क्षमता के होंगे, यदि by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2019BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019EXERCISE - JANUARY ATTEMPT (10 JAN, SHIFT-II )
30 Videos
- JEE MAIN 2019BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019EXERCISE - JANUARY ATTEMPT (11 JAN, SHIFT-I )
28 Videos
- JEE MAIN 2019BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019EXERCISE - JANUARY ATTEMPT (9 JAN, SHIFT-II)
30 Videos
- सॉल्वड पेपर 2017 (JEE MAIN ) BOOK - ARIHANT HINDICHAPTER - सॉल्वड पेपर 2017 (JEE MAIN ) EXERCISE - प्रश्न
30 Videos
- JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)BOOK - ARIHANT HINDICHAPTER - JEE MAIN 2019 (APRIL & JANUARY ATTEMPT)EXERCISE - JANUARY ATTEMPT (12 JAN, SHIFT -II)
30 Videos
Similar Questions
दो बल P तथा Q, जिनके परिमाण क्रमश: 2F तथा 3F हैं, परस्पर 9 कोण बनाते हैं। यदि बल Q को दोगुना कर दें, तो इनका परिणामी बल भी दोगुना हो जाता है। तब कोण θ होगा
View Solutiont=0 पर क्षैतिज से 60∘ के कोण पर 10 ms−1 के वेग से एक पिण्ड को प्रक्षेपित करते हैं। t=1s पर प्रक्षेप्य पथ की वक्रता त्रिज्या R है। वायु प्रतिरोध को नगण्य मानकर तथा गुरुत्वीय त्वरण g=10ms−2 लेकर R का मान है
View Solutionदो समतल दर्पणों (M1 तथा M2) को परस्पर ऐसे कोण पर रखा गया है, जिससे प्रकाश की एक किरण जब M2 के समान्तर जाती हुई M1 पर आपतित होती है, तो अन्ततः वह M2 से M1 के समान्तर परावर्तित होती है। दर्पणों के बीच के कोण का मान होगा
View Solutionएक प्रेक्षक प्रकाश गति की आधी गति से 10 GHz आवृति के एक स्थिर सुक्ष्म तरंग स्रोत की तरफ जा रहा है। प्रेक्षक द्वारा माफी गयी सुक्ष्म तरंग की आवृति का मान होगा।
प्रकाश की चाल = 3×108ms
View Solutionएक m द्रव्यमान का अल्फा कण किसी अज्ञात द्रव्यमान के स्थिर नाभिक से एक-विमीय प्रत्यास्थ संघट्ट करके अपनी प्रारम्भिक गतिज ऊर्जा का 64% भाग क्षय करके ठीक विपरीत दिशा में प्रकीर्णित हो जाता है। नाभिक का द्रव्यमान होगा-
View SolutionIf X1 and X2 are the susceptibilities of a diamagnetic substance at a absoulte temperature T1 and T2 where T2>T1 then
View SolutionIn Arrhenius equation, If EA is positive and T2>T1, then ___________
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View SolutionIsothermal curves for a given mass of gas are shown at two different temperture T1andT2 in Fig. State whether T1>T2orT2>T1. Justify your answer.
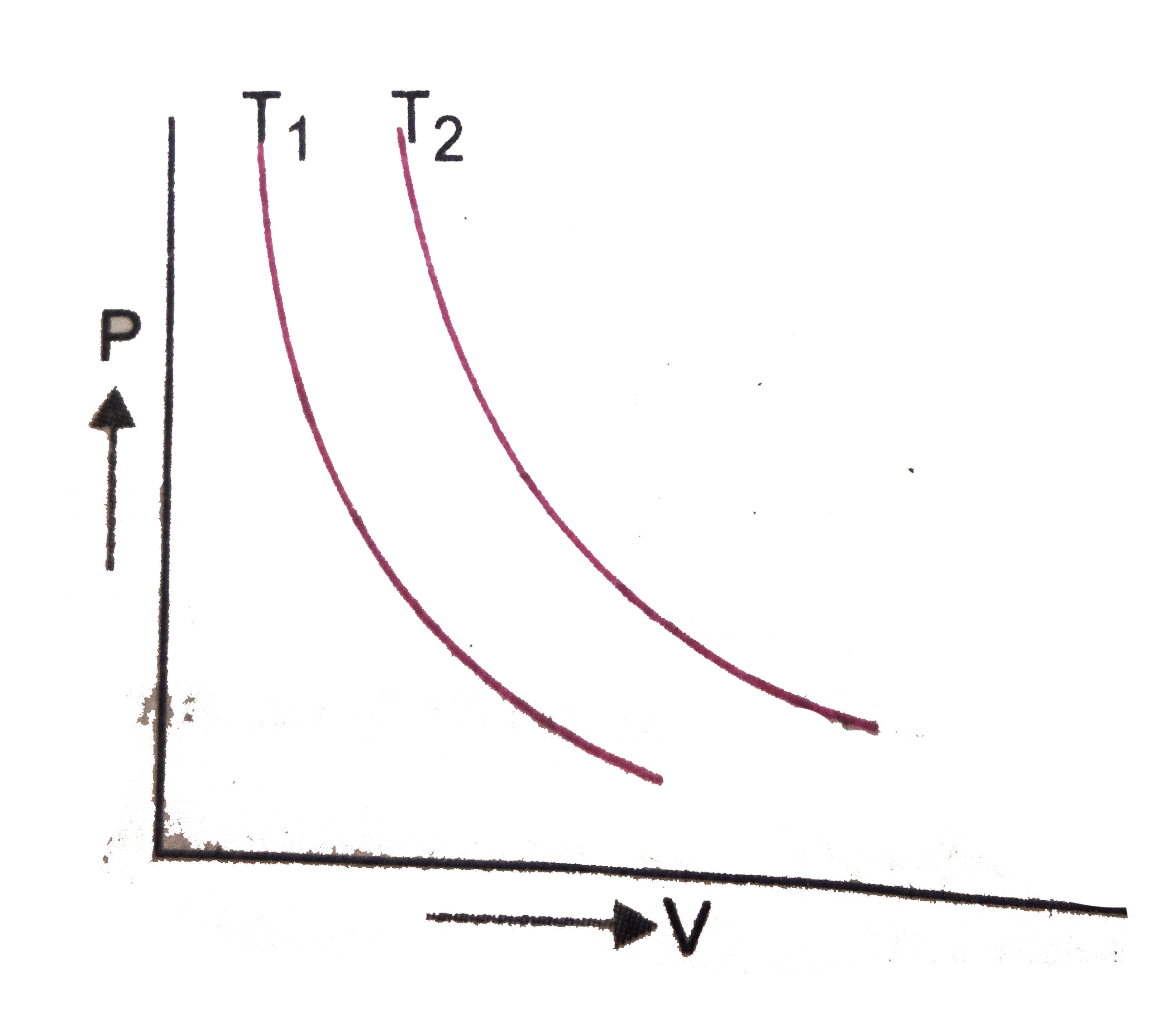
View SolutionIn the following graph, say whether T1>T2 or not.
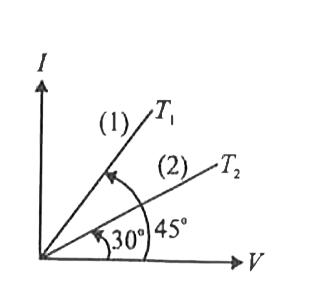
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
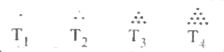
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View SolutionAn unstable nucleus decays in three different modes, each mode having a different half life T_(1), T_(2),T_(3)(T_(1)gt gt T_(2) gt gt T_(3)) . The overall half life of a sample will be given by
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View SolutionLet t1=(sin−1x)sin−1x,t2=(sin−1x)cos−1x,t3=(cos−1x)sin−1x,t4=(cos−1x)cos−1x
Match the items of Column I with the items Column II
Column-IColumn-IIA) x∈(0,cos1)p) t1>t2>t4>t3B) x∈(cos1,1√2)q) t4>t3>t1>t2C) x∈(1√2,sin1)r) t1>t2>t4>t3D) x∈(sin1,1)s) t3>t4>t1>t2
View Solution
