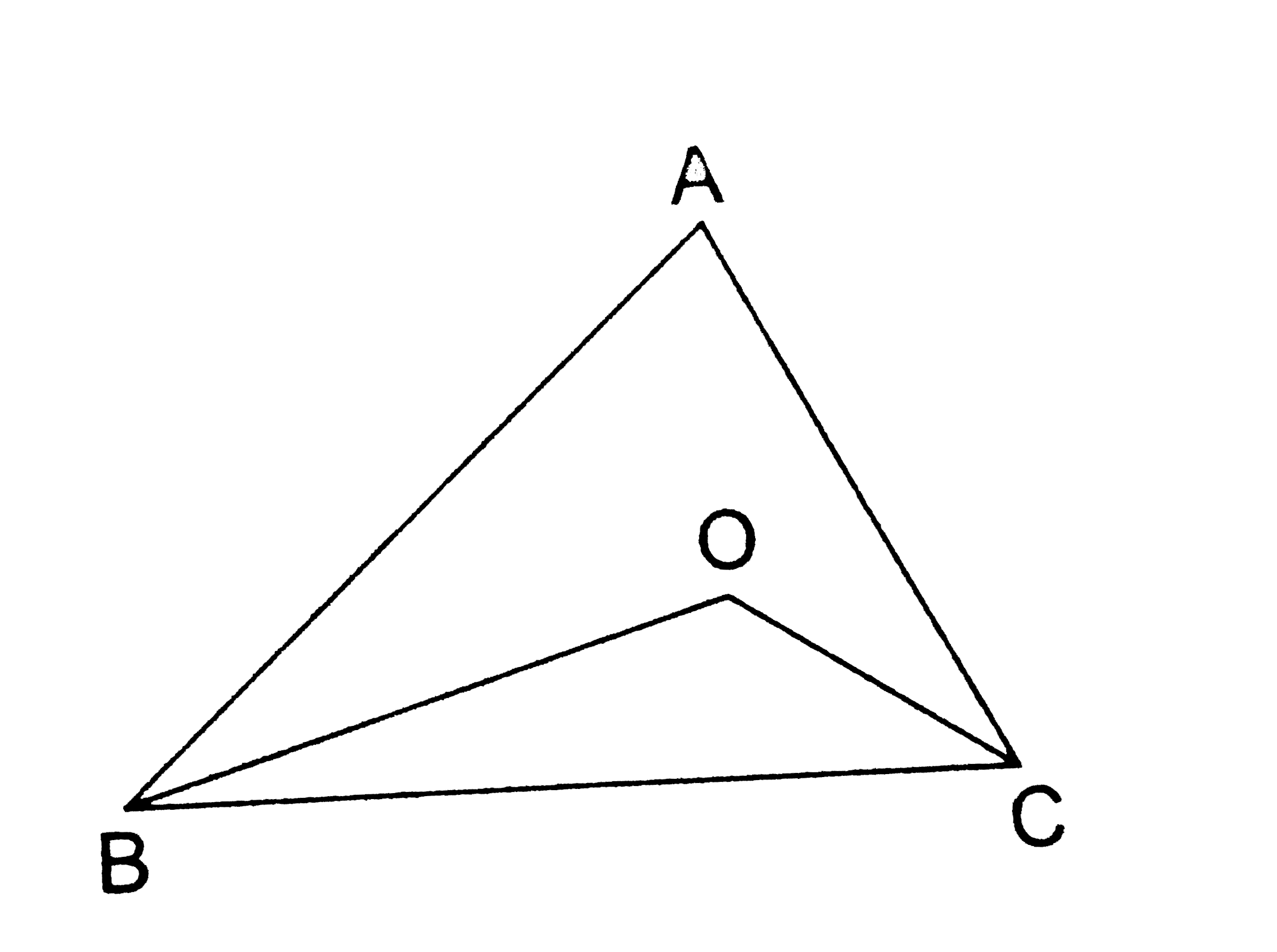
In ΔABC it is given that ∠A=70∘,∠B=52∘,BOandCO are the bisectors of ∠Band∠C respectively. Find ∠OCBand∠BOC.

A
29 and 125
B
26 and 125
C
56 and 125
D
58 and 56
Video Solution
Text Solution
The correct Answer is:A
We know that the sum of the angles of a triangle is 180∘.
∴∠A+∠B+∠C=180∘
⇒70∘+52∘+∠C=180∘
⇒∠C=(180∘−122∘)=58∘=29∘
and ∠OBC=12∠C=(12×58∘)=26∘. In ΔBOC, we have
∠OBC+∠OCB+∠BOC=180∘
26∘+29∘+∠BOC=180∘
⇒∠BOC=(180∘−55∘)=125∘.
Hence, ∠OCB=29∘and∠BOC=125∘.
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 8
13 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)
73 Videos
Similar Questions
Knowledge Check
In the given diagram of ΔABC,∠B=80∘,∠C=30∘ BF and CF are the angle bisectors of ∠CBDand∠BCE respectively. Find the value of ∠BFC :
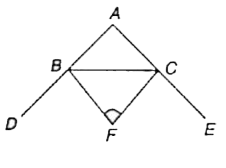 A110∘B50∘C125∘D55∘
A110∘B50∘C125∘D55∘In ΔABC, if ∠B<∠A then
ABC<CABBC<CACBC>AB+CADAB<CAIn the following figure ∠B=70∘ and ∠C=30∘.BOandCO are the angle bisectors of ∠ABCand∠ACB. Find the value of ∠BOC:
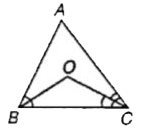 A30∘B40∘C120∘D130∘
A30∘B40∘C120∘D130∘
In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively. Prove that ∠AOB=12(∠C+∠D).
View SolutionIn ΔABC , if ∠A=62∘,∠B=28∘ then find ∠C
View SolutionIn a ΔABC, the bisectors of ∠Band∠C intersect each other point O. Then∠BOC is ?
View SolutionIn △ABC the bisectors of ∠B and ∠C intersect at I if ∠A=70∘ then ∠BIC=…………..
View SolutionIn ΔABC,BC=ABand∠B=80∘. Then, ∠A=?
View Solution