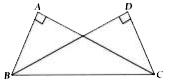
A $Δ A B C$ is right angled at A and L is a point on BC such that $A L ⊥ B C$ . Prove that $∠ B A L = ∠ A C B$ .

Video Solution

Text Solution

Verified by Experts

We know that in a right-angled trianlge, the sum of the two acute anlges is $90^{\circ}$ .
So, in right trianlge $Δ A L B$ , we have
$∠ B A L + ∠ A B L + = 90^{\circ} \Rightarrow ∠ B A L + ∠ A B C = 90^{\circ} ... ... (i)$
In right triangle BAC, we have
$∠ A B C + ∠ A C B = 90^{\circ} . ... . (i i)$
From (i) and (ii), we get
$∠ B A L + ∠ A B C = ∠ A B C + ∠ A C B$ .
Hence, $∠ B A L + ∠ A C B$ .

Updated on:21/07/2023

|

Class 9 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

$Δ A B C$ is right angled at A and $A D ⊥ B C$ . Then $\frac{B D}{D C} =$
A ${(\frac{A B}{A C})}^{2}$
B $\frac{A B}{A C}$
C ${(\frac{A B}{A D})}^{2}$
D $\frac{A B}{A D}$
$Δ A B C$ is right angled at A. if AB = 24 mm and AC = 7 mm, then BC is
A20 mm
B25 mm
C30 mm
D35 mm

RS AGGARWAL-TRIANGLES-EXAMPLE

Home
Ask Doubt
Profile