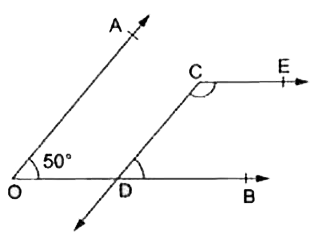
Calculate and in the adjoining figure, it is being given that and is a straight line.
Video Solution
Text Solution
Since AOB is a straight line, the sum of all the angles on the lower side of AOB at a point O on it, is .
.
Again, AOB is a straight line and O is a point on it. So, the sum of all angles on the upper side of AOB at a point O on it, is .
,
.
|
Topper's Solved these Questions
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Example
13 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A
12 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)
24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)
18 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle, ∠ACB=54∘ and BCF is a straight line. Find x.
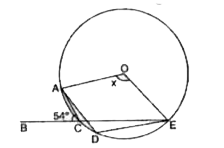 A126∘B54∘C108∘D90∘
A126∘B54∘C108∘D90∘In the adjoining figure, POQ is a straight line. Find the m and n when m:n=7:5
 A105∘,65∘B106∘,75∘C105∘,75∘D105∘,95∘
A105∘,65∘B106∘,75∘C105∘,75∘D105∘,95∘
In the adjoining figure, AOB is a straight line. Find the value of x.
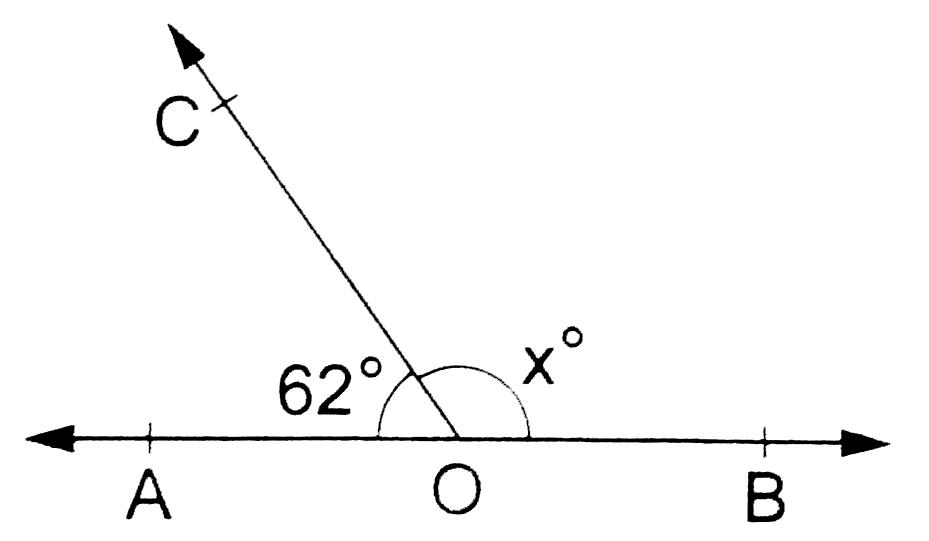
View SolutionIn the given figure, AOB is a straight line. If ∠AOC=4x∘ and ∠BOC=5x∘ then ∠AOC=?
View SolutionIn the given figure, AN=AC,∠BAC=52∘,∠ACK=84∘ and BCK is a straight line.Prove that NB=NC
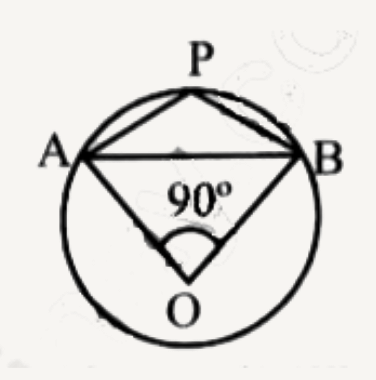
View SolutionIn the given figure, O is the centre of the circle, ∠AOB=90∘. Find ∠APB :
View SolutionIn the given figure, AOB is a straight line. If ∠AOC=(3x+10)∘ and ∠BOC=(4x−26)∘, then ∠BOC= ?

View SolutionIn the adjoining figure, Find the values of x and y, Given that AOD is a straight line.
View Solution