In an equilateral triangle prove that the centroid and the centre of the circumcircle (circumcentre) coincide.

Video Solution

Text Solution

Verified by Experts

The point of intersection of the medians of a triangle is called its centroid. The centroid of a triangle is the point located at $\frac{2}{3}$ of the distance from a vertex along a median. The center of the circumcircle of this triangle is called the circumcentre.
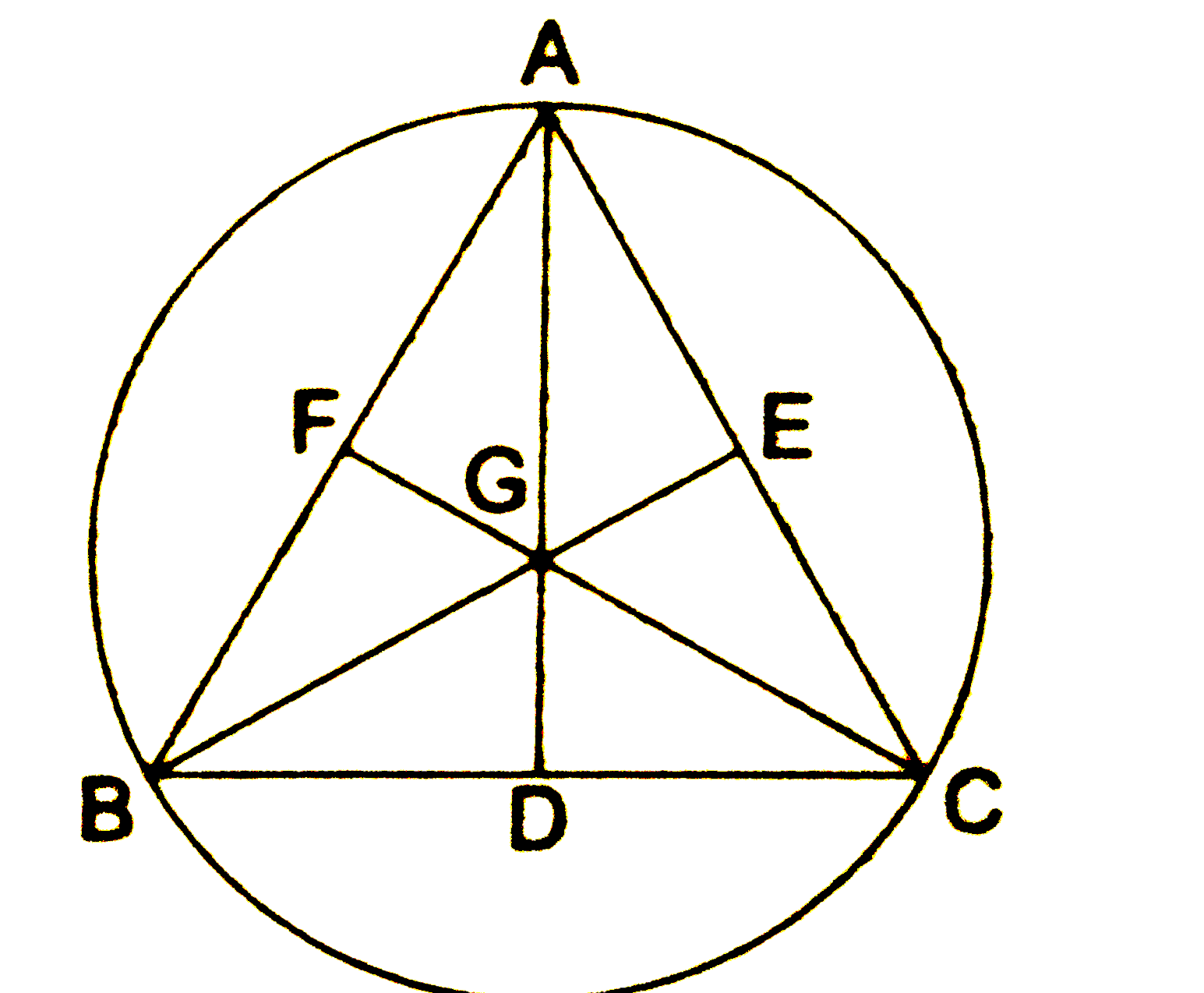
Let $Δ A B C$ be the given equilateral triangle and let its medians $A D, B E$ and $C F$ intersect at $G$ .
Then $G$ is the centroid of $Δ A B C$ .
In $Δ B C E$ and $Δ C B F$ we have
$B C$ $=$ $C B$ [common]
$∠ B = ∠ C$ [ each equal to $60^{\circ}]$
$C E = B E [A C = A B \Rightarrow \frac{1}{2} A C = \frac{1}{2} A B]$
$∴ Δ A B C = C F$
Similarly, $A D = B E$ .
Thus, $A D = B E = C F \Rightarrow \frac{2}{3} A C = \frac{1}{2} A B]$
$\Rightarrow G A = G B = G C$
This shows that $G$ is the circumcentre of $Δ A B C$
Hence, $G$ is the centroid as well as circumcentre of $Δ A B C$ .

Updated on:21/07/2023

In an equilateral triangle, the incentre, circumcentre, orthocentre and centroid are :
Acollinear
Bconcyclic
Ccoincide
Dnone of these
In an equilateral triangle, the incentre, circumcentre, orthocentre and centroid are :
Aconcylic
Bcoincident
Ccollinear
Dnone of these
In an equilateral triangle, the inradius, circumradius, and one of the exradii are in the ratio
Aconcylic
Bcoincident
Ccollinear
Dnone of these