Match the Column I with Column II
For a satellite in circular orbit

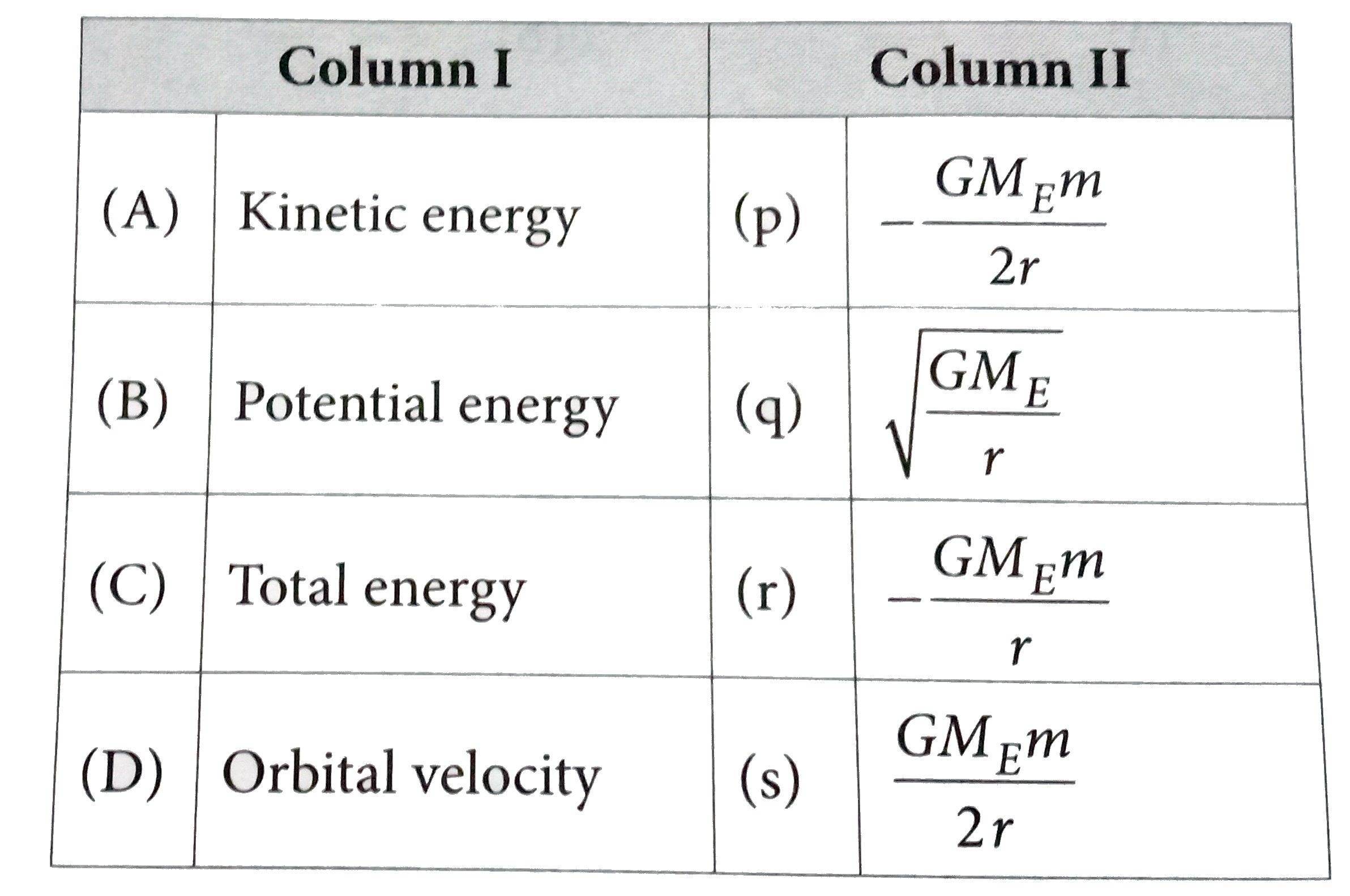
(where $M_{E}$ is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )

A

Kinetic energy $= - \frac{G M_{E} m}{2 r}$

B

Potential energy $= \frac{G M_{E} m}{2 r}$

C

Total energy $= - \frac{G M_{E} m}{r}$

D

Orbital velocity $= \sqrt{\frac{G M_{E}}{r}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Potential energy $= \frac{G M_{E} m}{2 r}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A satellite is revolving in circular orbit of radius $r$ around the earth of mass M. Time of revolution of satellite is
A $T \propto \frac{r^{5}}{G M}$
B $T \propto \sqrt{\frac{r^{3}}{G M}}$
C $T \propto \sqrt{\frac{r}{\frac{G M^{2}}{3}}}$
D $T \propto \sqrt{\frac{r^{3}}{\frac{G M}{4}}}$
Question 2 - Select One
A satellite moves around the earth in a circular orbit with speed $v$ . If $m$ is the mass of the satellite, its total energy is
A $- \frac{1}{2} m v^{2}$
B $\frac{1}{2} m v^{2}$
C $\frac{3}{2} m v^{2}$
D $\frac{1}{4} m v^{2}$
Question 3 - Select One
The period of a satellite in a circular orbit of radius R is T. The period of another satellite in circular orbit of radius 4 R is :
A4 T
BT/4
CT/8
D8 T

MTG GUIDE-GRAVITATION-CHECK YOUR NEET VITALS

Home
Ask Doubt
Profile