x>1 के लिए व्यंजक 2log10x−logx(0.01) का निम्नतम है
2
4
6
8
The correct Answer is:B
Step by step video, text & image solution for xgt1 के लिए व्यंजक 2log_(10)x-log_(x)(0.01) का निम्नतम है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- लघुगणक और आंशिक भिन्नें BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - SOLVED MULTIPLE CHOICE QUESTIONS (लघुगणक )
24 Videos
- लघुगणक और आंशिक भिन्नें BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - SOLVED MULTIPLE CHOICE QUESTIONS (आंशिक भिन्ने)
11 Videos
- फलन, सीमा, सांतत्य तथा अवकलनीयताBOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( MATCH THE COLUMN TYPE)
13 Videos
- वर्ग समीकरण एवं असमिकायें BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)
2 Videos
Similar Questions
y=logax के परिभाषित होने के लिए 'a' निश्चित रूप से होना चाहिए
View Solutionयदि 2x+3(x+1)(x−3)=ax+1+bx−3 तो a+b=
View Solutionकॉलम I में दिए गए वक्तव्यों/व्यंजकों का कॉलम II में दिये गये मानों से सुमेल करे।
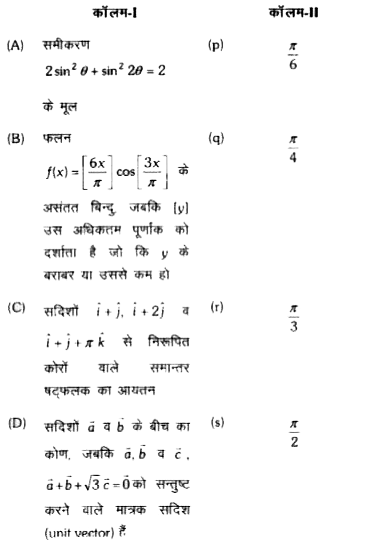
View Solution
View SolutionIf log10x−log10√x=2logx10, then possible value of x is given by
View Solutionsolve for x:2log_(10)x-log_(x)(0.01)=5
View SolutionFor x>1, the minimum value of 2log10(x)−logx(0.01) is
View Solutionlog_(10)^(x)-log_(10)sqrt(x)=2log_(x)10. Find x
View SolutionThe equation (log_(10)x+2)^(3)+(log_(10)x-1)^(3)=(2log_(10)x+1)3
View SolutionFor x>1, show that: 2log10x−logx0.01≥4
View SolutionThe value of p in R for which the equation sin^(-1)((log_(10)x)^(2)-2log_(10)x+2)+tan^(-1)((log_(10)x)^(2)-2log_(10)x+2)+cos^(-1)((log_(10)x)^(2)-2(log_(10)x))=p possess solution is
View SolutionSelect the correct answer (MCQ) :
(iv) The least value of the quantity 2log10(x)−logx(0.01)[x>1]=
View Solutionλ का वह धनात्मक मान जिसके लिए व्यंजक x2(√x+λx2)10 में x2 का गुणांक 720 है, है
View Solutionx>1 के लिए व्यंजक 2log10x−logx(0.01) का निम्नतम है
View Solutionm का वह मान, जिसके लिए फलन
f(x)={mx2x≤12xx>1 x=1 पर अवकलनीय हो है
View SolutionA function f(x) , Is defined as follows for real x f(x)={(1-x^(2), xlt1 के लिए ),(0,x=1 के लिए),(1+x^(2),xgt1 के लिए):} Then
View Solution
