If the speed of a car increases 4 times, the stopping distance ( in m) for this will increase by _________ .
The correct Answer is:16
To solve the problem, we need to understand the relationship between the speed of a car and its stopping distance. The stopping distance is the distance a car travels before it comes to a complete stop after the brakes are applied.
1. Understanding the Relationship:
The stopping distance (s) of a vehicle is related to its speed (v) by the equation derived from the equations of motion. Specifically, we can use the formula:
v2=u2+2as
where:
- v = final velocity (which is 0 when the car stops)
- u = initial velocity
- a = acceleration (which is negative in the case of deceleration)
- s = stopping distance
2. Setting Up the Initial Conditions:
Since the car is initially at rest, we can assume:
- Initial speed u=0
- Let the initial speed be v1 and the stopping distance be s1.
3. Considering the Increased Speed:
According to the problem, the speed of the car increases 4 times. Therefore, the new speed v2 can be expressed as:
v2=4v1
4. Applying the Relationship:
From the stopping distance formula, we can express the stopping distances in terms of the speeds:
v21∝s1andv22∝s2
Therefore, we can write:
v21v22=s1s2
5. Substituting for v2:
Substitute v2=4v1 into the equation:
v21(4v1)2=s1s2
Simplifying this gives:
v2116v21=s1s2
This reduces to:
116=s1s2
6. Finding the Stopping Distance Ratio:
Rearranging gives:
s2=16s1
This means that the stopping distance increases by a factor of 16 when the speed of the car increases 4 times.
Final Answer:
The stopping distance will increase by 16 times.
The stopping distance (s) of a vehicle is related to its speed (v) by the equation derived from the equations of motion. Specifically, we can use the formula:
v2=u2+2as
where:
- v = final velocity (which is 0 when the car stops)
- u = initial velocity
- a = acceleration (which is negative in the case of deceleration)
- s = stopping distance
Since the car is initially at rest, we can assume:
- Initial speed u=0
- Let the initial speed be v1 and the stopping distance be s1.
According to the problem, the speed of the car increases 4 times. Therefore, the new speed v2 can be expressed as:
v2=4v1
From the stopping distance formula, we can express the stopping distances in terms of the speeds:
v21∝s1andv22∝s2
Therefore, we can write:
v21v22=s1s2
Substitute v2=4v1 into the equation:
v21(4v1)2=s1s2
Simplifying this gives:
v2116v21=s1s2
This reduces to:
116=s1s2
Rearranging gives:
s2=16s1
This means that the stopping distance increases by a factor of 16 when the speed of the car increases 4 times.
The stopping distance will increase by 16 times.
Topper's Solved these Questions
Similar Questions
An auto rickshaw takes 3 hours to cover a distance of 36 km. If its speed is increased by 4 km/h, the time taken by it to cover the same distance is __________.
View SolutionA car starts from rest and accelerates uniformly to a speed 50ms−1 over a distance of 250m . The speed of car is increased to 60ms−1 within 10s,if the acceleration is further increased. Find this acceleration and the distance travelled by car in 10s .
View Solution
Knowledge Check
If the units of M and L are increased three times, then the unit of energy will be increased by
A3 timesB6timesC27 timesD81 timesIf the units M and L are increased three times, then the units of energy will be increased by
A3 timesB6 timesC27 timesD81 timesTripling the speed of a motor car multiplies the distance required for stopping it by
A2B3C6D9
A car covers a distance of 240km with some speed . If the speed is increased by 20km/hr, it will cover the same distance in 2 hours less find the speed of the car .
View SolutionA toy car is moving away from a wall, as shown in the given figure. As time increases, the distance of the car from the wall also increases, as depicted in the graph. The hypothesis that can be derived from the given graph is
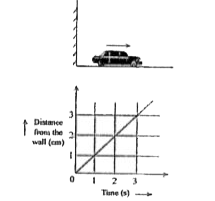
View SolutionTripling the speed of a motor car multiplies the distance required for stopping it by
View SolutionTripling the speed of the motor car multiplies the distance needed for stopping it by
View SolutionTripling the speed of the motor car multiplies the distance needed for stopping it by
View Solution
