L लम्बाई व M चुंबकीय आधूर्ण की छड़ को मोड़कर अर्ध-वृत्ताकार बनाया गया है, तो इसका चुंबकीय आधूर्ण होगा
M
2Mπ
Mπ
Mπ
The correct Answer is:B
छड़ को मोड़ने पर ध्रुव सामर्थ्य अपरिवर्तित रहेगी जबकि चुंबकीय आघूर्ण बदल जाएगा। नया चुंबकीय आघूर्ण M.=m(2R)=m(2Lπ)=2Mπ

Topper's Solved these Questions
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Ordinary Thinking (भू-चुंबकत्व)
24 Videos
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Ordinary Thinking (चुंबकीय उपकरण )
40 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - SELF EVALUATION TEST
16 Videos
- तरंग प्रकाशिकी BOOK - ERRORLESS HINDICHAPTER - तरंग प्रकाशिकी EXERCISE - तरंग प्रकाशिकी(SELF EVALUATION TEST )
21 Videos
Similar Questions
एक चुम्बकीय सुई क्षैतिज समतल में घूम सकती है। यदि इसे किसी भू-चुम्बकीय ध्रुव पर ले जायें तो यह
View Solutionदोलन चुंबकत्वमापी का आवर्तकाल T0 है। इसकी चुंबक एक अन्य चुंबक से बदल दी जाती है, जिसका जड़त्व आघूर्ण पहले की तुलना में 3 गुना तथा चुंबकीय आघूर्ण 1/3 गुना है। अब नया आवर्तकाल होगा
View Solution5×10−3kgm2 जड़त्व आघूर्ण का एक पहिया 20 चक्कर/सैकण्ड की दर से घूर्णन गति कर रहा है। इसे 20 सैकण्ड में विरामावस्था में लाने के लिये आवश्यक कोणीय मंदन का मान होगा
View Solutionनिम्न चित्र में स्रोत S1 एवं S2 सभी दिशाओं में λ तरंगदैर्ध्य का प्रकाश उत्सर्जित करते हैं। ये स्रोत पूर्णतः समान कला में हैं एवं इनके बीच की दूरी 1.5λ है। यदि हम दर्शित आरम्भ बिन्दु से पथ 1 एवं 2 के अनुदिश जायें तो व्यतिकरण के कारण सदैव उच्चिष्ठ प्राप्त होगा
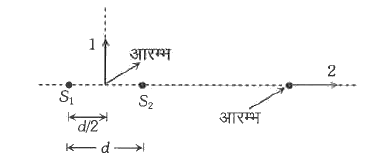
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के कारण चुंबकीय क्षेत्र।
View Solutionपरिनालिका | धारवाहक वृत्ताकार पाश के कारण चुंबकीय क्षेत्र
View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionप्रस्तावना |चुंबकीय क्षेत्र की अवधारणा
View Solutionचुंबकीय क्षेत्र की अवधारणा
View Solutionविद्युत धारावाही वृत्ताकार पाश के केन्द्र पर चुंबकीय क्षेत्र
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View Solutionअनन्त लम्बाई के ठोस बेलनाकार चालक का चुंबकीय क्षेत्र
View Solution
