In a modified YDSE, monochromatic uniform and parallel beam of light of wavelength 6000A∘ and intensity (10π)W/m2 is incident normally on two circular apertures A and B of radii 1 mm and 2 mm respectively. Find the ratio of the intensity of the sources [IBIA] ?Solution in Telugu
The correct Answer is:4
Step by step video, text & image solution for In a modified YDSE, monochromatic uniform and parallel beam of light of wavelength 6000 A^(@) and intensity ((10)/(pi)) W//m^(2) is incident normally on two circular apertures A and B of radii 1 mm and 2 mm respectively. Find the ratio of the intensity of the sources [(I_(B))/(I_(A))] ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Practice Sheet Exercise - II (DIFFRACTION) (Level - I (Main) (Straight objective Type questions)
3 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Practice Sheet Exercise - II (DIFFRACTION)(Level - II ) (Straight objective Type questions)
1 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Linked Comprehension Type Questions
3 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
81 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
Light waves of wave length λ propagate in a medium. If M and N are two points on the wave front and they are separated by a distance λ/4, the phase difference between them will be (in radian)
View SolutionIn YDSE ten maxima of two slit pattern (Interference) if formed in central maxima of single slit pattern diffraction. If separation in between two slits is 1mm, then what is the width of each slit ?
View SolutionIn the arrangement shown, a screen is placed normal to the line joining the two point coherent sources S1 and S2. The interference pattern consist of concentric circles. λ is the wavelength of light (D>>d).

The phase difference of the interfering light at point P is
View SolutionA wave is described by the equation
y=(1.0mm)sinπ(x2.0cm−10.01s)
Find the time period and the wavelength.
View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train (V = 330 m/s)
View SolutionA monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I_(0) , find the point on the screen at which intensity is I_(0) and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t = 6 mu m, d = 1 mm, and D = 1 m, where d and D have their usual meaning. Give your answer in mm.
View SolutionIn YDSE, D = 2 mm, D = 2 m, and lambda = 500 nm . If intensities of two slits are I_(0) and 9I_(0) , then find intensity at y = (1)/(6) mm .
View SolutionIn a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
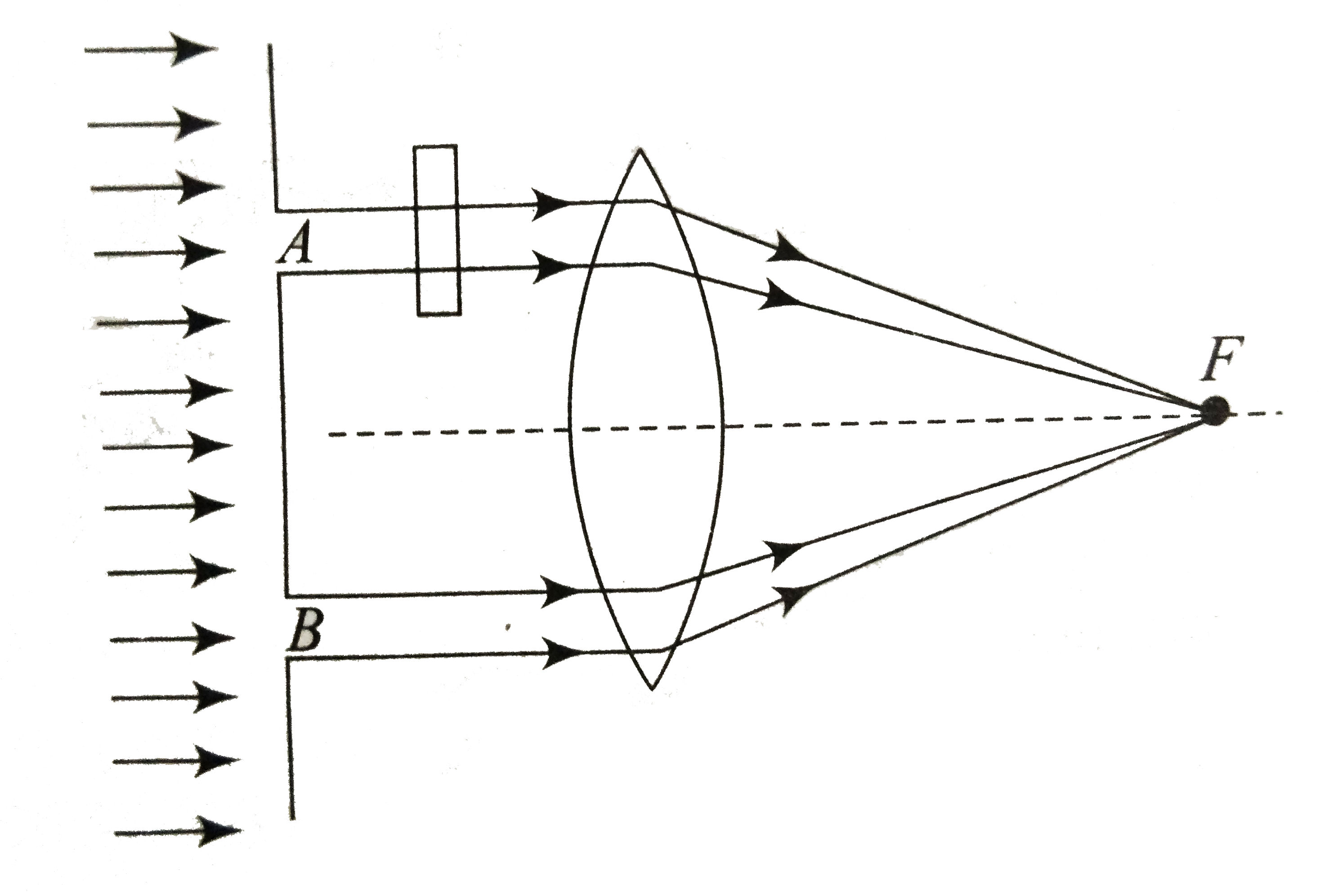
View SolutionA parallel beam of uniform, monochromatic light of wavelength 6600 Å has an intensity of 900Wm−2. The number of photons in 1mm3 of this radiation are 1×10X then find out value of X.
View SolutionIn a modified Young's double slit experiment a monochromatic uniform and parallel beam of light of wave length 6000Å and intensity (10π)Wm−2 is incident normally on two circular apertures A and B of radii 20009Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture. A. Calculate the power (in watt) received at the focal spot F of the lens. The lens is symmertrically placed with respect to the apertures. Assume that 10% of the power received by each aperture goes in the originally direction and is brought to the focal spot.
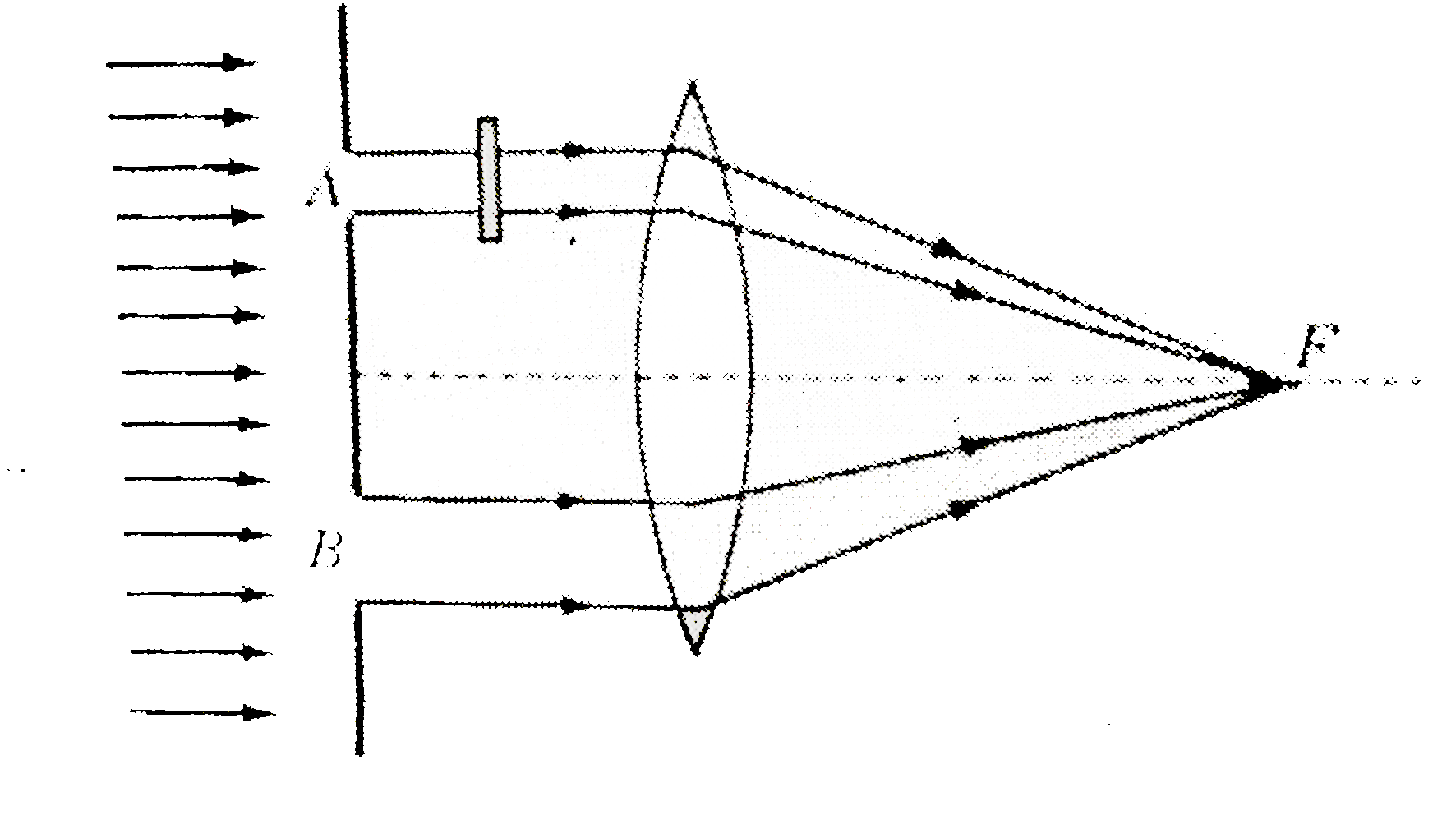
View SolutionA parallel beam of uniform,monochromatic light of wavelenth 2640 A has an intensity of 200W/m2. The number of photons in 1mm3 of this radiation are .................
View SolutionThe intensity ratio of the two interfering beams of light is m. What is the value of Imax−Imin/Imax+Imin?
View SolutionTwo beams of light of intensity I_(1), and I_(2) interfere to give an interference pattern. If the ratio of maximum intensity to that of minimum intensity is (16)/(4) then I_(1):I_(2)= .......
View SolutionIn a modified YDSE, monochromatic uniform and parallel beam of light of wavelength 6000 A^(0) and intensity (10/pi) W//m^(2) is incident normally on two circular apertures A and B of radii 1 mm and 2 mm respectively. Find the ratio of the intensity of the two sources [(I_(B))/(I_(A))]
View SolutionIn a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000 Å and intensity (10//pi) W m^(-2) is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000 Å and refractive index 1.5 for the wavelength of 6000 Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
View Solution
