Let [x] denote the greatest integer less than or equal to x for any real number x. then limx→∞[n√2]n is equal to
0
2
√2
1
The correct Answer is:C
To solve the limit limn→∞(√2n)n, where (⋅) denotes the greatest integer function, we can follow these steps:
Step 1: Understand the Expression
The expression we need to evaluate is (√2n)n. Here, (√2n) is the greatest integer less than or equal to √2n.
Step 2: Analyze √2n
As n approaches infinity, √2n grows exponentially. Specifically, we know that:
√2n=2n/2
Thus, as n increases, √2n becomes very large.
Step 3: Apply the Greatest Integer Function
The greatest integer function (√2n) can be approximated as:
(\sqrt{2}^n) \approx \sqrt{2}^n \quad \text{(as n becomes very large)}
This means that:
(√2n)=√2n−ϵn
where 0≤ϵn<1.
Step 4: Substitute into the Limit
Now we can substitute this approximation into our limit:
limn→∞(√2n)n=limn→∞√2n−ϵnn
This can be simplified to:
limn→∞(√2nn−ϵnn)
Step 5: Evaluate Each Part of the Limit
1. Evaluate limn→∞√2nn:
- Since √2n grows exponentially while n grows linearly, this limit approaches infinity:
limn→∞√2nn=∞
2. Evaluate limn→∞ϵnn:
- Since ϵn is bounded (it is less than 1), this limit approaches 0:
limn→∞ϵnn=0
Step 6: Combine the Results
Putting it all together, we have:
limn→∞(√2nn−ϵnn)=∞−0=∞
Conclusion
Thus, the limit is:
limn→∞(√2n)n=∞
The expression we need to evaluate is (√2n)n. Here, (√2n) is the greatest integer less than or equal to √2n.
As n approaches infinity, √2n grows exponentially. Specifically, we know that:
√2n=2n/2
Thus, as n increases, √2n becomes very large.
The greatest integer function (√2n) can be approximated as:
(\sqrt{2}^n) \approx \sqrt{2}^n \quad \text{(as n becomes very large)}
This means that:
(√2n)=√2n−ϵn
where 0≤ϵn<1.
Now we can substitute this approximation into our limit:
limn→∞(√2n)n=limn→∞√2n−ϵnn
This can be simplified to:
limn→∞(√2nn−ϵnn)
1. Evaluate limn→∞√2nn:
- Since √2n grows exponentially while n grows linearly, this limit approaches infinity:
limn→∞√2nn=∞
- Since ϵn is bounded (it is less than 1), this limit approaches 0:
limn→∞ϵnn=0
Putting it all together, we have:
limn→∞(√2nn−ϵnn)=∞−0=∞
Thus, the limit is:
limn→∞(√2n)n=∞
Topper's Solved these Questions
- LIMITS AND CONTINUITYBOOK - MTG-WBJEECHAPTER - LIMITS AND CONTINUITYEXERCISE - WE JEE PREVIOUS YEARS QUESTIONS (CATEGORY 2 : SINGLE OPTION CORRECT TYPE)
5 Videos
- LIMITS AND CONTINUITYBOOK - MTG-WBJEECHAPTER - LIMITS AND CONTINUITYEXERCISE - WE JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
2 Videos
- LIMITS AND CONTINUITYBOOK - MTG-WBJEECHAPTER - LIMITS AND CONTINUITYEXERCISE - WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
10 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - MTG-WBJEECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - WB JEE Previous Years Questions ( CATEGORY 1 : Single Option Correct Type (1 Mark))
6 Videos
- LOGARITHMS BOOK - MTG-WBJEECHAPTER - LOGARITHMS EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS
10 Videos
Similar Questions
Knowledge Check
If [x] denotes the greatest integer less than or equal to x for any real number x. Then, limx→∞[n√2]n is
A0B2C√2D1Let [x] be the greatest integer less than or equal to x, for a real number x. Then the following sum
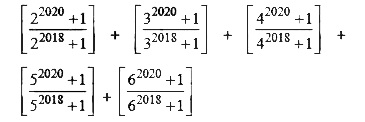
is-A80B85C90D95Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
Acontinuous at x = 0Bcontinuous in (−1,0)Cdifferentiable at x = 1Ddifferentiable in (−1,1)
Let [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
View SolutionLet [x] be the greatest integer less than or equal to x, for a real number x. Then the equation [x2]=x+1 has
View SolutionLet [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
View SolutionLet [x] denote the greatest integer less than or equal to x. Then, ∫1.50[x]dx=?
View SolutionLet [x] denote the greatest integer less than or equal to x. Then, ∫−11[x]dx=?
View Solution
