Two identical circular loops, P and Q each of radius r and carrying currents I and 2I respectively are lying in parallel planes such that they have a common axis. Their centres are distance 2r apart. The direction of current in both the loops is clockwise as seen from O which is equidistant from both the loops. Find the magnitude of the net magnetic field at point O.

Field due to loop P=μOIr22(r2+r2)3/2(downwards)
Field due to loop Q=μo2Ir22(r2+r2)3/2 (downward)
So, net field at O will be downward
=μoIr22(2r2)3/2+μo2Ir22(r2+r2)3/2
=μoIr2(2r2)3/2(12+2)=5μoIr223/2r3.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - [Set-III]
6 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) [SET - I]
32 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
8 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Two identical circular loops, P and Q, each of radius r and carrying currents I and 2 I respectively are lying in parallel planes such that they have a common axis. The direction of current in both the loops in clockwise as seen from O, which is euqidistant from both loops. Find the magnitude of the net magnetic field at point O.

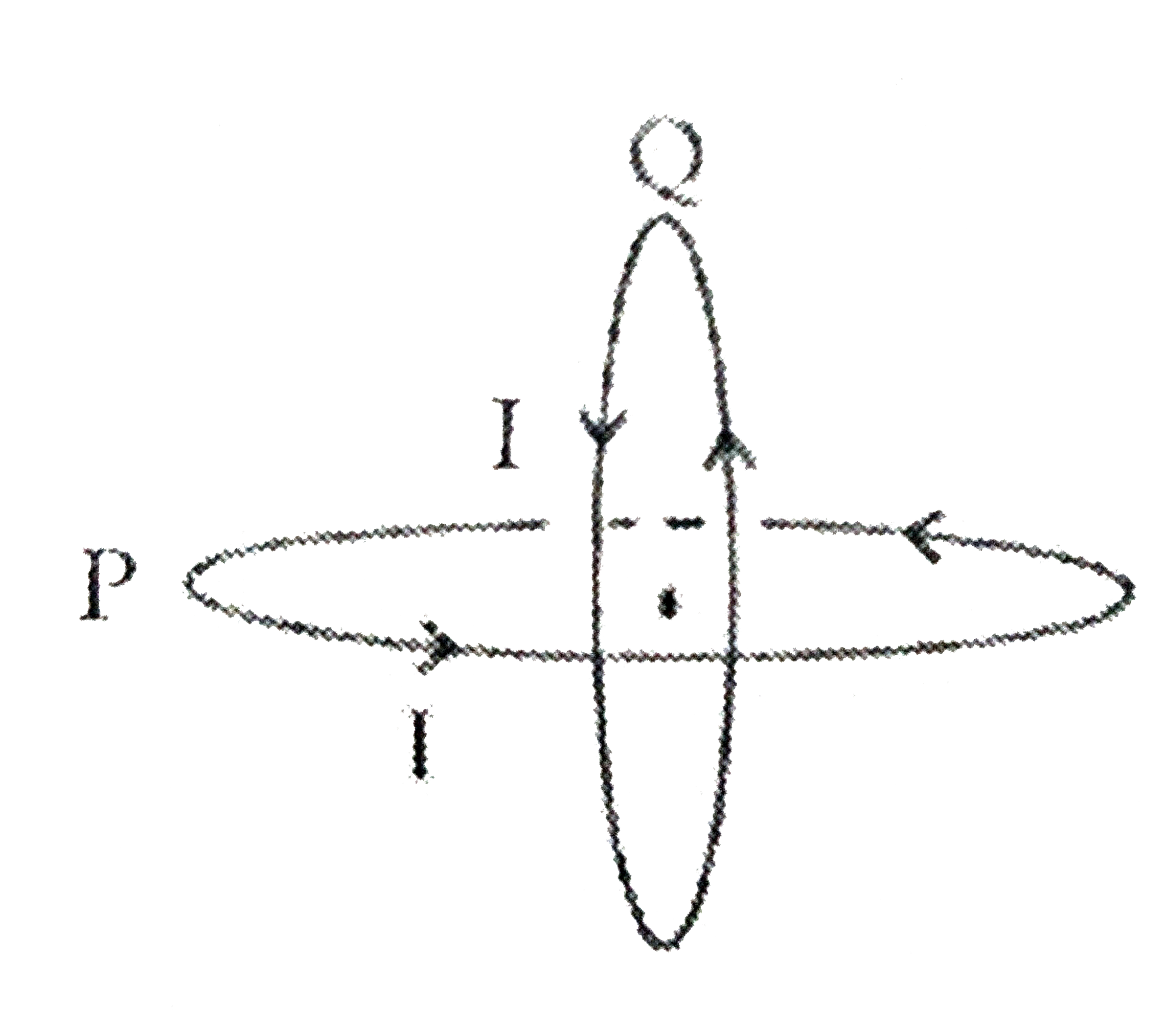
View SolutionTwo identical circular loops P and Q carrying equal currents are placed such that their geometrical axis are perpendicular to each other as shown in figure. And the direction of current appear’s anticlockwise as seen from point O which is equidistant from loop P and Q. Find the magnitude and direction of the net magnetic field produced at the p oint O.
tanθ=B2B1=1,θ=π/4.
View Solution
Knowledge Check
A circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.BzeroCinversely proportional to r.Ddirectly proportional to I.Magnetic field intensity H at the centre of a circular loop of radius r carrying current I e.m.u. is
ArI oerstedB2πr oerstedCI2πr oerstedD2πrI oersted
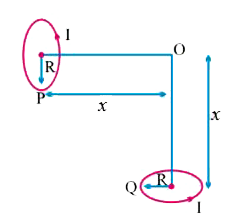
Two identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in fig. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
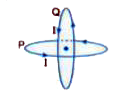
View SolutionTwo identical loops P and Q each of radius 5cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to 3A and 4A respectively.
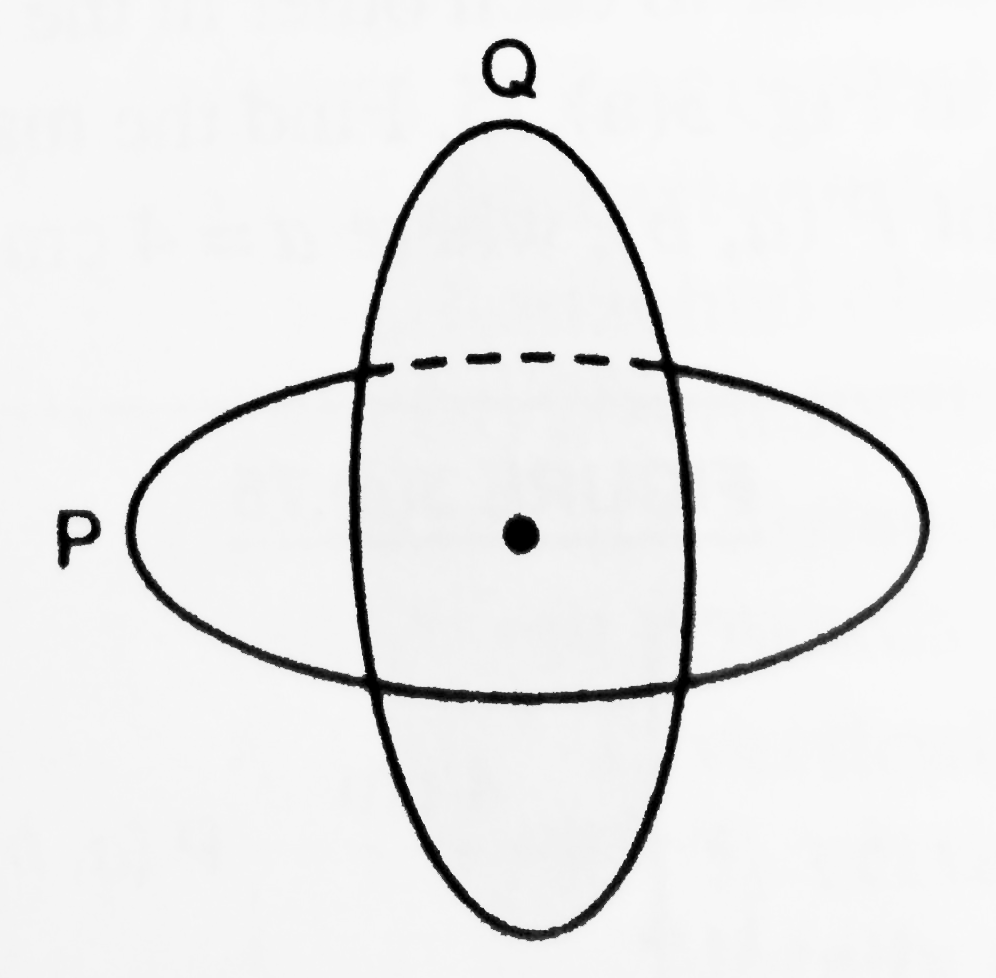
View SolutionTwo identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common centre. Find the magnitude and PC direction of the magnetic field at the common centre of the two coils, if they carry currents equal to land √3I respectively.
View SolutionWhat is the magnetic moment of a circular loop of radius R carrying current I clockwise?
View SolutionA circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .
View Solution
