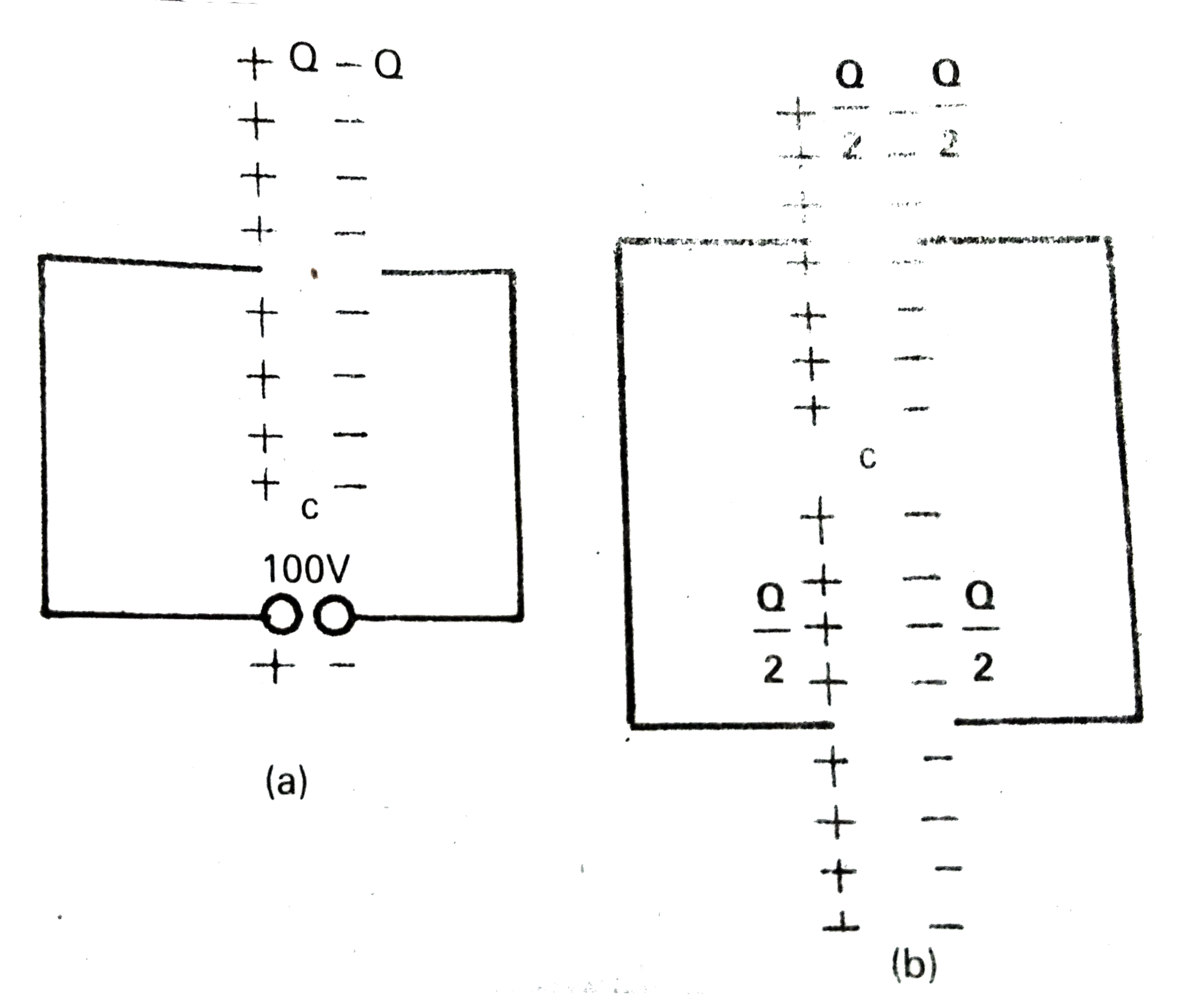
(a) A 900 pF capacitor is charged by 100 V battery [Fig. 2.31(a)]. How much electrostatic energy is stored by the capacitor?
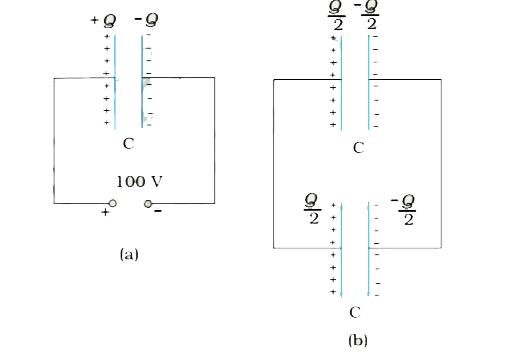
(b) The capacitor is disconnected from the battery and connected to another 900 pF capacitor [Fig. 2.31(b)]. What is the electrostatic energy stored by the system?
![(a) A 900 pF capacitor is charged by 100 V battery [Fig. 2.31(a)]. How much electrostatic energy is stored by the capacitor? (b) The capacitor is disconnected from the battery and connected to another 900 pF capacitor [Fig. 2.31(b)]. What is the electrostatic energy stored by the system?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_GUJ_PHY_XII_P1_C02_SLV_010_Q01.png) Solution in Gujrati
Solution in Gujrati
(a) The charge on the capacitor is
Q = CV = 900×10−12F×100V=9×10−8C
The energy stored by the capacitance is
=(1/2)CV2=(1/2)QV=(1/2)×9×10−8C×100V=4.5×10−6 J
(b) In the steady situation, the two capacitors have their positive plates at the same potential, and their negative plates at the same potential. Let the common potential difference be V′. The charge on each capacitance is then Q.=CV.. By charge conservation, Q.=Q/2. This implies V.=V/2. The total energy of the system is =2×12Q.V.=14QV=2.25×10−6 J
Thus in going from (a) to (b), though no charge is lost, the final energy is only half the initial energy. Where has the remaining energy gone? There is a transient period before the system settles to the situation (b). During this period, a transient current flows from the first capacitor to the second. Energy is lost during this time in the form of heat and electromagnetic radiation.
Topper's Solved these Questions
- BOOK - NCERT GUJARATICHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ADDITIONAL EXERCISES1videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT GUJARATICHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISES35videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT GUJARATICHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ADDITIONAL EXERCISES5videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT GUJARATICHAPTER - MAGNETISM AND MATTEREXERCISE - Additional Exercises19videos
MAGNETISM AND MATTER
Similar Questions
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9 C from a point P (0, 0, 3 cm) to a point Q (0, 4 cm, 0), via a point R (0, 6 cm, 9 cm)
03:39View SolutionTwo charges 5×10−8 C and −3×10−8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
06:06View SolutionSuppose that the electric field part of an electromagnetic wave in vacuum is →E={(3.1N/C)cos[(1.8rad/m)y+(5.4×106rad/s)]}ˆi
What is the direction of propagation ?03:39View SolutionWhy does a paramagnetic sample display greater magnetisation (for the same magnetising field) when cooled?
01:22View SolutionA 900 pF capacitor is charged by 100V battery.
(a) How much electrostatic energy is strored by the capacitor ? The capacitor is disconnected from the battery and connected to another 900 pF capacitor. How much is the electrostatic energy stored in the system ?04:15View SolutionA 900pF capacitor is charged by 100 V battery. How much electros-tatic energy is stored by the capacitor?
(b) The capacitor is disconnected from the battery and connected to another 900 pF. Capacitor. What is the electrostatic energy stored by the system?
 02:19View Solution
02:19View SolutionA 900 pF capacitor is charged by 100V battery.
(a) How much electrostatic energy is strored by the capacitor ? The capacitor is disconnected from the battery and connected to another 900 pF capacitor. How much is the electrostatic energy stored in the system ?04:35View SolutionA 900 pF capacitor is charged by a 100 V battery. How much electrostatic energy is stored in the capacitor?
04:05View SolutionA 900 pF capacitor is charged by a 100 V battery. The capacitor is disconnected from the battery and is then connected to another 900 pF capacitor. What is the electrostatic energy stored by the system?
04:47View SolutionA 900 pF capacitor is charged by a 100 V battery. The electrostatic energy stored by the capacitor is
01:17View Solution(a) A 900 pF capacitor is charged by 100 V battery [Fig. 2.31(a)]. How much electrostatic energy is stored by the capacitor?
(b) The capacitor is disconnected from the battery and connected to another 900 pF capacitor [Fig. 2.31(b)]. What is the electrostatic energy stored by the system?
 05:22View Solution
05:22View SolutionA 900 pF capacitor is charged by 100V battery.
(a) How much electrostatic energy is strored by the capacitor ? The capacitor is disconnected from the battery and connected to another 900 pF capacitor. How much is the electrostatic energy stored in the system ?02:04View Solution(a) A 900 pF capacitor is charged by 100 V battery [Fig. 2.31(a)]. How much electrostatic energy is stored by the capacitor?
(b) The capacitor is disconnected from the battery and connected to another 900 pF capacitor [Fig. 2.31(b)]. What is the electrostatic energy stored by the system?
 04:31View Solution
04:31View SolutionA 900 pF (PiCo farad) capacitor is charged by 100 V (Volt) battery How much electrostatic energy is stored by the capacitor ?
07:06View SolutionA 900 pF (PiCo farad) capacitor is charged by 100 V (Volt) battery The capacitor is now disConnected from the battery and is Connected to another uncharged 900pF (PiCo farad) capacitor. How much is the electrostatic energy stored in the system?
01:13View Solution
