When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. If the distance to the floor is 76 cm and for rotation less than 1 rev, what are the (a) smallest and (b) largest angular speeds that cause the toast to hit and then topple to be butter-side down?
To solve the problem of the buttered toast falling off the counter and determining the smallest and largest angular speeds that cause it to hit and then topple butter-side down, we will follow these steps:
Step 1: Calculate the time of fall
We know the height h=0.76m and the acceleration due to gravity g=10m/s2. The time t it takes to fall can be calculated using the formula:
t=√2hg
Substituting the values:
t=√2×0.7610=√1.5210=√0.152≈0.389s
Step 2: Calculate the smallest angular speed (ωmin)
For the toast to hit the ground butter-side down with the smallest angular speed, it needs to rotate π2 radians (90 degrees) during its fall. Using the relationship:
θ=ωt
we can rearrange to find ω:
ωmin=θmint
Substituting θmin=π2 and t=0.389:
ωmin=π20.389≈1.57080.389≈4.04rad/s
Step 3: Calculate the largest angular speed (ωmax)
For the toast to hit the ground butter-side down with the largest angular speed, it needs to rotate 3π2 radians (270 degrees) during its fall. Using the same relationship:
ωmax=θmaxt
Substituting θmax=3π2 and t=0.389:
ωmax=3π20.389≈4.71240.389≈12.10rad/s
Final Answers
(a) The smallest angular speed ωmin is approximately 4.04 rad/s.
(b) The largest angular speed ωmax is approximately 12.10 rad/s.
We know the height h=0.76m and the acceleration due to gravity g=10m/s2. The time t it takes to fall can be calculated using the formula:
t=√2hg
Substituting the values:
t=√2×0.7610=√1.5210=√0.152≈0.389s
For the toast to hit the ground butter-side down with the smallest angular speed, it needs to rotate π2 radians (90 degrees) during its fall. Using the relationship:
θ=ωt
we can rearrange to find ω:
ωmin=θmint
Substituting θmin=π2 and t=0.389:
ωmin=π20.389≈1.57080.389≈4.04rad/s
For the toast to hit the ground butter-side down with the largest angular speed, it needs to rotate 3π2 radians (270 degrees) during its fall. Using the same relationship:
ωmax=θmaxt
Substituting θmax=3π2 and t=0.389:
ωmax=3π20.389≈4.71240.389≈12.10rad/s
(a) The smallest angular speed ωmin is approximately 4.04 rad/s.
(b) The largest angular speed ωmax is approximately 12.10 rad/s.
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
43 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
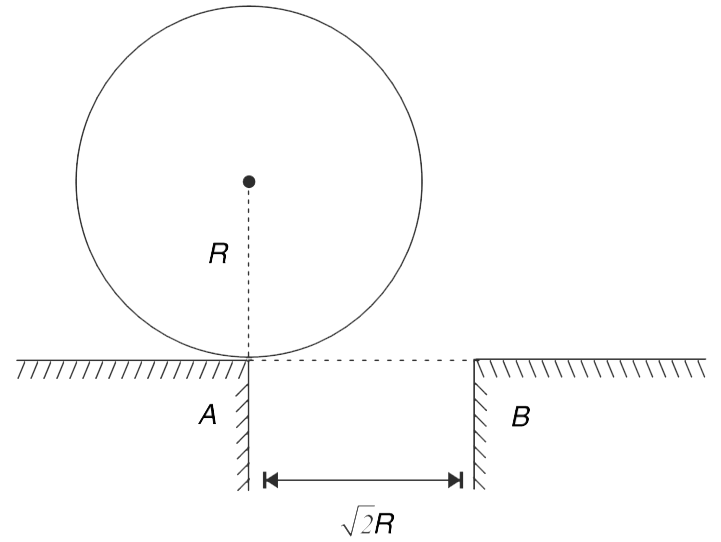
A disc of radius R stands at the edge of a table. If the given a gentle push and it beings to fall. Assume that the disc does not slip at A and it rotates about the point as it falls. The falling disc hits the edge of another table placed at same height as the first one at a horizontal distance of √2R. Imagine that the disc hits the edge B and rotates (up) about the edge
(a) Find the speed of the centre of the disc at the instant just before it hits the edge B.
(b) Find the angular speed of the disc about B just after the hit.
View SolutionA uniform cubical block of mass M and side length L is lying on the edge of a rough table with 14th of its edge overhanging. When a small block of mass m is placed on its top surface at the right edge (see fig.), the cube is on verge of toppling. The block of mass m is given a sharp horizontal impulse so that it acquires a velocity towards B. The small block moves on the top surface and falls on the other side. What is maximum coefficient of friction between the small block and the cube so that the cube does not rotate as the block moves over it. Assume that the friction between the cube and the table is large enough to prevent sliding of the cube on the table.

View Solution
Knowledge Check
When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. If the distance to the floor is 80cm and for rotation less than 1rev, what are the
(i) smallest and
(ii) largest angular speeds that cause the toast to hit and then topple to be butter-side down ?Asmallest angular speed is 5π4rad/s and largest angular speed is 15π4rads.Bsmallest angular speed is π4rad/s and largest angular speed is 3π4rad/sCsmallest angular speed is π2rad/s and largest angular speed is 3π2rad/s.Dsmallest angular speed is 5π2rad/s and largest angular speed is 15π2rad/s.Consider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
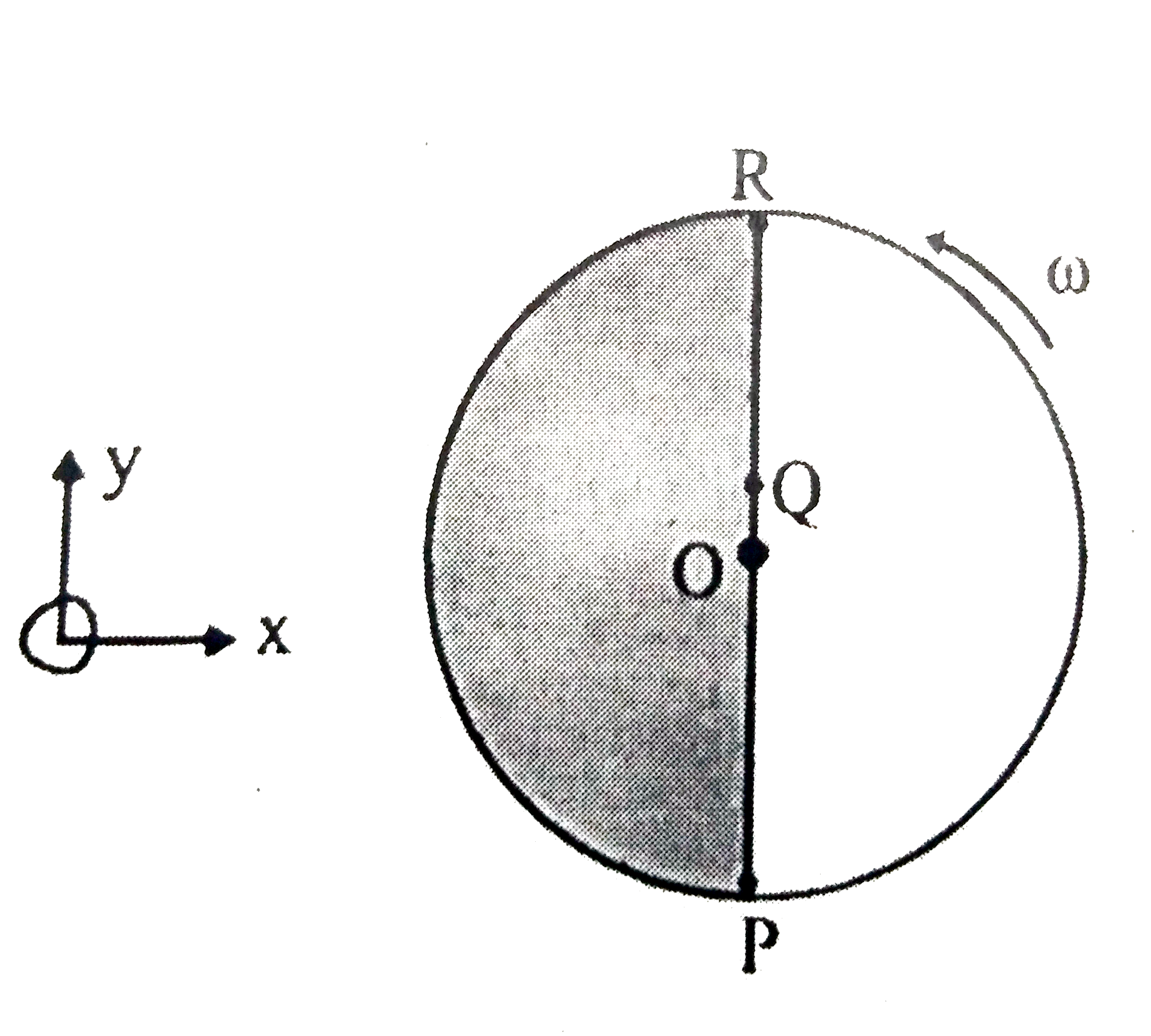 AP lands in the shaded region and Q in the unshaded region.BP lands in the unshaded region and Q in the shaded region.CBoth P and Q land in the unshaded region.DBoth P and Q land in the shaded region.
AP lands in the shaded region and Q in the unshaded region.BP lands in the unshaded region and Q in the shaded region.CBoth P and Q land in the unshaded region.DBoth P and Q land in the shaded region.Consider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then
 Ap lands in the shaded region and Q in the unshaded region.Bp lands in the unshaded region and Q in the shaded regionCBoth p and Q land in the unshaded region.DBoth p and Q Jand in the shaded region
Ap lands in the shaded region and Q in the unshaded region.Bp lands in the unshaded region and Q in the shaded regionCBoth p and Q land in the unshaded region.DBoth p and Q Jand in the shaded region
Figure 6-47 shows three crates being pushed over a concrete floor by a horizontal force F of magnitude 425 N. The masses of the crates are m1=30.0kg,m2=10.0kg,andm3=20.0kg The coefficient of kinetic friction between the floor and each of the crates is 0.700. (a) What is the magnitude F32 of the force on crate 3 from crate 2? (b) If the crates then slide onto a polished floor, where the coefficient of kinetic friction is less than 0.700, is magnitude F32 more than, less than, or the same as it was when the coefficient was 0.700?

View SolutionEven some seasoned roller coaster riders blanch at the thought of riding the Rotor, which is essentially a large, hollow cylinder that is rotated rapidly around its central axis. Before the ride begins, a rider enters the cylinder through a door on the side and stands on a floor, up against a canvas covered wall. The door is closed, and as the cylinder begins to turn, the rider, wall, and floor move in unison. When the rider's speed reaches some predetermined value, the floor abruptly and alarminglly falls away. The rider does not fal with it but instead is pinned to the wall while the cylinder rotates, as if an unseen (and somewhat unfriendly) agent is pressin the body to the wall. Later, the floor is eased back to the rider's feet, the cylinder slows. and the rider sinks a few centimeters to regain footing on the floor. (Some riders consider all this to be fun.)
Suppose that the coefficient of static friction μs between the rider's clothing and the canvas is 0.40 and that the cylinder's radius R is 2.1 m.
a. What minimum speed v must the cylinder and rider have if the rider is not to fall when the floor drops?
b. If the rider's mass is 49 kg, what is the magnitude of the centripetal force on her?
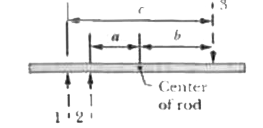
View SolutionFigure 10-61 is an overhead view of a rod of length 1.0 m and mass 1.0 kg that is lying stationary on a frictionless surface when three bullets hit it simultaneously. The bullets move along paths that are in the plane of the rod and per-pendicular to the rod. Bullet 1 has mass 10 g and speed 2.0 m/s. Bullet 2 has mass 20 g and speed 3.0 m/s. Bullet 3 has mass 30 g and speed 5.0 m/s. The labelled distance are α=10cm, b = 60 cm, and c = 80 cm. As a result of the impacts, the rod-bullets system rotates around its center of mass while the center of mass moves in a straight line over the frictionless surface. (a) What is the linear speed of the system's center of mass? (b) What is the distance between the rod's center and the system's center of mass ? ( c) What is the rotational inertia of the system about the system's center of mass?
View SolutionTwo blocks of mass m1=10kg and m2=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. the table is rotating with an angular velocity of 10rad/s. about a vertical axis passing through its center O. the masses are placed along the diameter of the table on either side of the center O such that the mass m1 is at a distance of 0.124m from O. the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m/s2).
(a) Calculate the friction on m1
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on m1.
View SolutionConsider a disc rotating in the horizontal plane with a constant angular speed ω about its centre O . The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 18 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then

View Solution
